Skip to main content
Loading...

Another Strategy

What other strategies are used for calculating volume?

Goal:

Goal:

Let’s take a look at the previous shape.

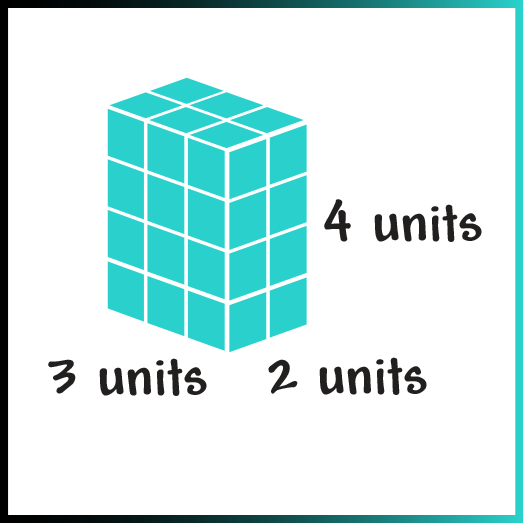
A geometric shape with 4 cubes tall, 3 cubes across and 2 cubes in depth.

How can you determine the volume of this shape without counting cubes? Work through the slides below to learn more about calculating volume using a formula

Counting Cubes

To calculate the volume of this shape you would count the number of cubes across the length, the width, and the height. Altogether, there are 24 cubes in this shape. Now, these same dimensions can be used to calculate the volume without needing to count every cube.

Using Dimensions

Dimensions are the measurements of a shape’s sides. As you counted the squares to determine the volume of the example shape, you used three dimensions: the length, width, and height. In this case, the length is 3 units, the width is 2 units, and the height is 4 units, .

A geometric shape with 4 cubes tall, 3 cubes across and 2 cubes in depth.

Now What?

Now that you have identified the dimensions of the shape, which math operation will be used to calculate the volume? Hint: Notice that each layer of cubes that fills the shape is an equal group.

Putting It All Together

A geometric shape with 4 cubes tall, 3 cubes across and 2 cubes in depth.

The dimensions of the shape are:

  • length: 3 units
  • width: 2 units
  • height: 4 units

Multiply the dimensions of the shape to determine the volume.

\(\large\mathsf{ V = 3\times2\times4=24 }\)

The volume of the shape is 24 units\(\mathsf{ ^3 }\). Both strategies, counting cubes and using the formula, reached the conclusion that the volume of the shape is 24 units\(\mathsf{ ^3 }\).

Why are the units for volume cubed (units\(\mathsf{ ^3 }\))?  
Your Response Answer

It is because you are multiplying the same unit 3 times: unit x unit x unit = units\(\mathsf{ ^3 }\).

In this case, the volume will be 3 units x 2 units x 4 units = 24 units\(\mathsf{ ^3 }\).