Assess Yourself
How well do you understand the ideas in this lesson?
Goal:
Goal:
Are you ready to take this lesson's quiz? These questions will help you find out. Go back to the lesson if you do not know an answer.
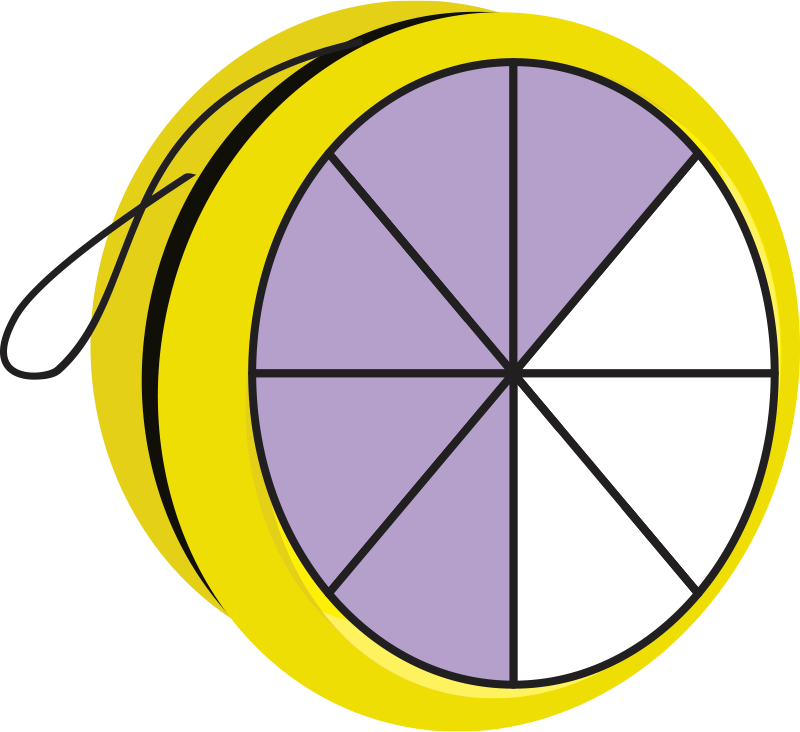
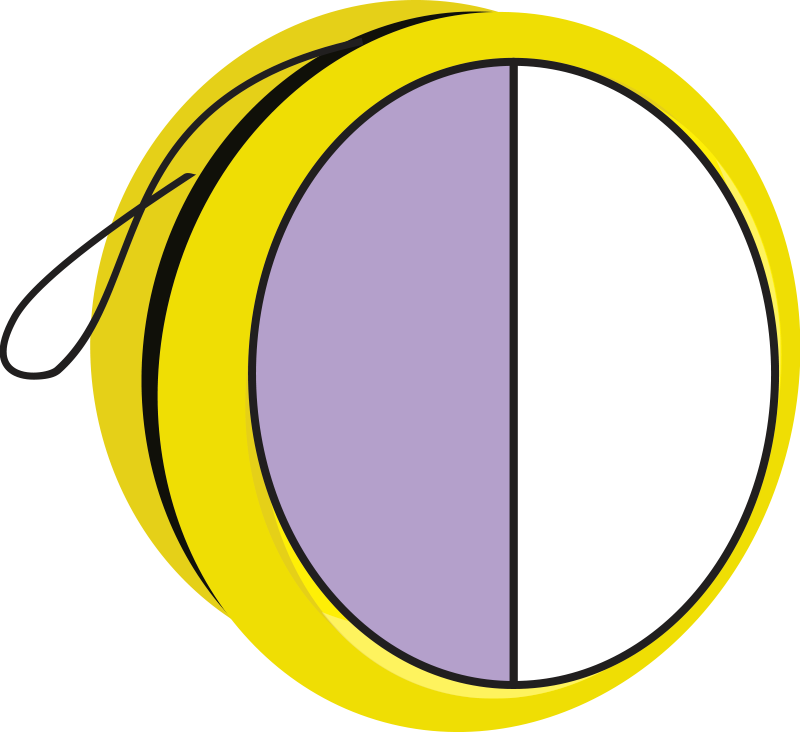
2 of the 4 parts of this yo-yo are shaded. Which yo-yo has an equivalent fraction?
Sorry, this fraction is not equivalent because it does not have the same amount of shaded area.
Sorry, this fraction is not equivalent because it does not have the same amount of shaded area.
Sorry, this fraction is not equivalent because it does not have the same amount of shaded area.
Yes! This fraction is equivalent because it shows the same amount of shaded area.
Which fraction is equivalent to \({ \frac{2}{6} }\)

Sorry, that is not correct. These fractions are not equivalent because they name different amounts.
Yes! \({ \frac{2}{6} }\) is equivalent to \({ \frac{1}{3} }\) because they name the same amount.
Sorry, that is not correct. These fractions are not equivalent because they name different amounts.
Sorry, that is not correct. These fractions are not equivalent because they name different amounts.
Which equivalent fractions match this real-life example?
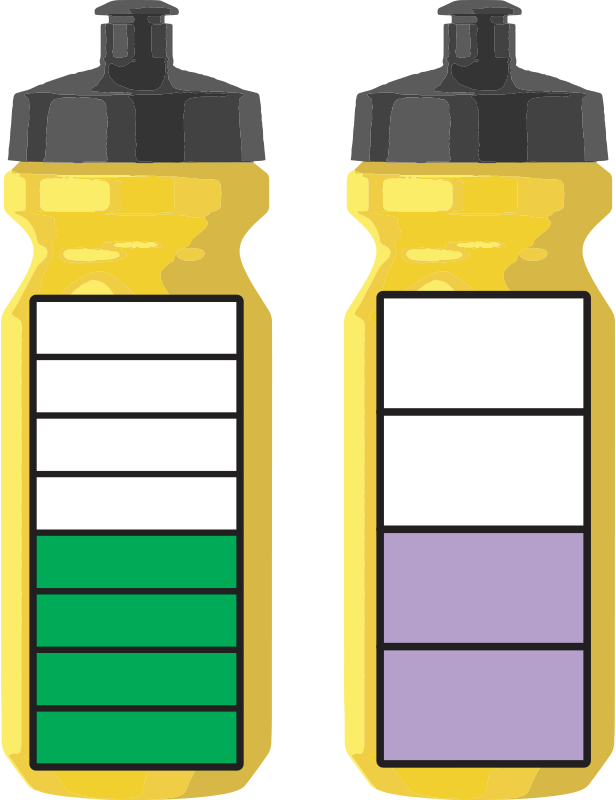
Two water bottles. Left bottle has 8 equal parts with 4 filled in. Right bottle has 4 equal parts with 2 filled in.
- \({ \frac{2}{4} = \frac{5}{8} }\)
- \({ \frac{3}{3} = \frac{4}{8} }\)
- \({ \frac{4}{8} = \frac{2}{4} }\)
- \({ \frac{4}{8} = \frac{1}{4} }\)
Sorry, that is not correct. These fractions show that \({ \frac{4}{8} }\) is equivalent to \({ \frac{2}{4} }\).
Sorry, that is not correct. These fractions show that \({ \frac{4}{8} }\) is equivalent to \({ \frac{2}{4} }\).
Yes! \({ \frac{4}{8} }\) is equivalent to \({ \frac{2}{4} }\).
Sorry, that is not correct. These fractions show that \({ \frac{4}{8} }\) is equivalent to \({ \frac{2}{4} }\).
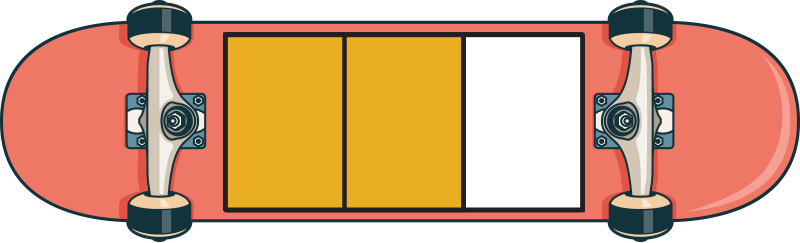
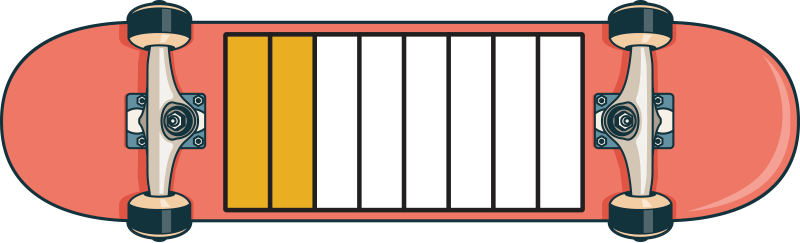
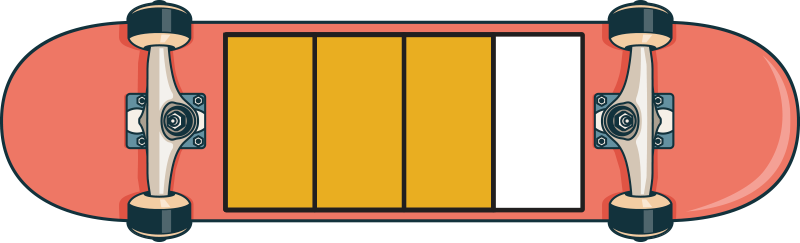
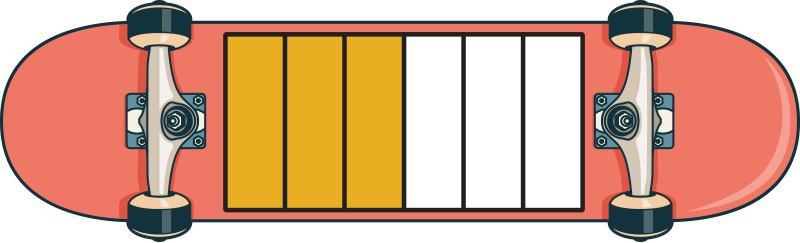
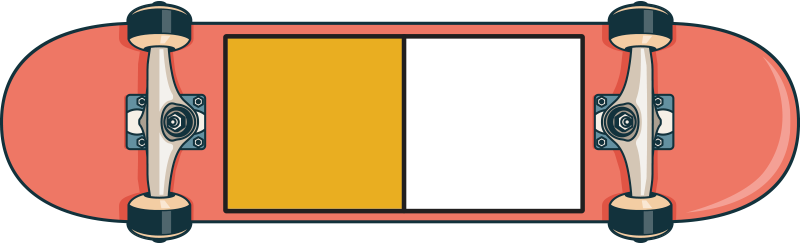
Half of this skateboard is shaded. Which skateboard has an equivalent fraction?
Sorry, this fraction is not equivalent because it does not have the same amount of shaded area.
Sorry, this fraction is not equivalent because it does not have the same amount of shaded area.
Sorry, this fraction is not equivalent because it does not have the same amount of shaded area.
Yes! This fraction is equivalent because it shows the same amount of shaded area.
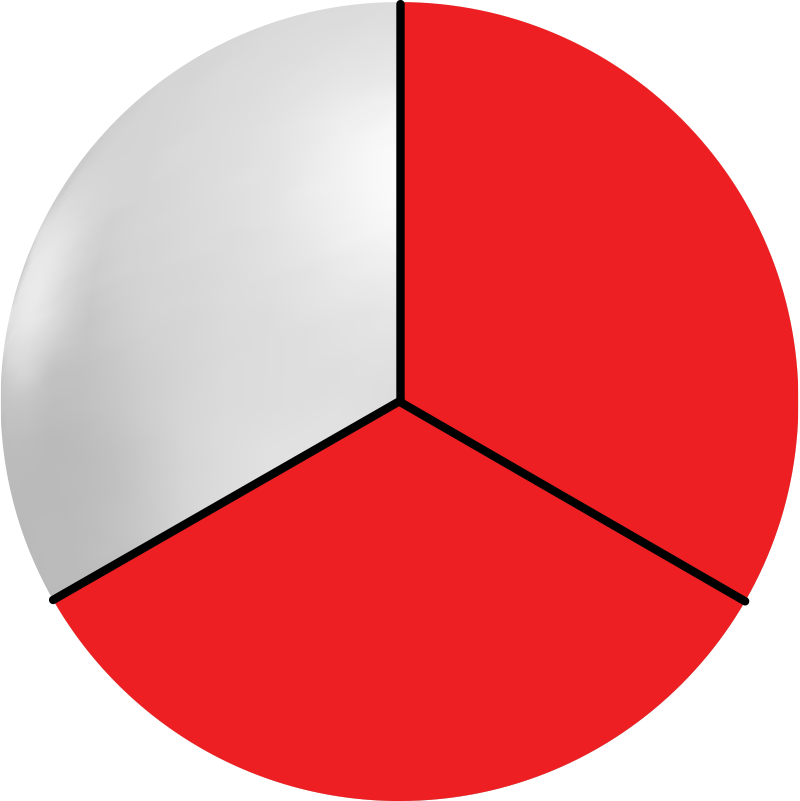
Which fraction is equivalent to \({ \frac{3}{6} }\)?

Yes! \({ \frac{2}{4} }\) is equivalent to \({ \frac{3}{6} }\) because they name the same amount.
Sorry, that is not correct. These fractions are not equivalent because they name different amounts.
Sorry, that is not correct. These fractions are not equivalent because they name different amounts.
Sorry, that is not correct. These fractions are not equivalent because they name different amounts.
Which equivalent fractions match this real-life example?

Two trucks. Left truck: Carrying a rectangle partitioned into 3 equal parts with 0 filled in. Righ truck: Carrying a rectangle partitioned into 4 equal parts with 0 filled in.
- \({ \frac{0}{3} = \frac{0}{4} }\)
- \({ \frac{7}{8} = \frac{1}{2} }\)
- \({ \frac{3}{8} = \frac{3}{6} }\)
- \({ \frac{2}{4} = \frac{1}{8} }\)
Yes! \({ \frac{0}{3} }\) is equivalent to \({ \frac{0}{4} }\).
Sorry, that is not correct. These fractions show that \({ \frac{0}{3} }\) is equivalent to \({ \frac{0}{4} }\).
Sorry, that is not correct. These fractions show that \({ \frac{0}{3} }\) is equivalent to \({ \frac{0}{4} }\).
Sorry, that is not correct. These fractions show that \({ \frac{0}{3} }\) is equivalent to \({ \frac{0}{4} }\).
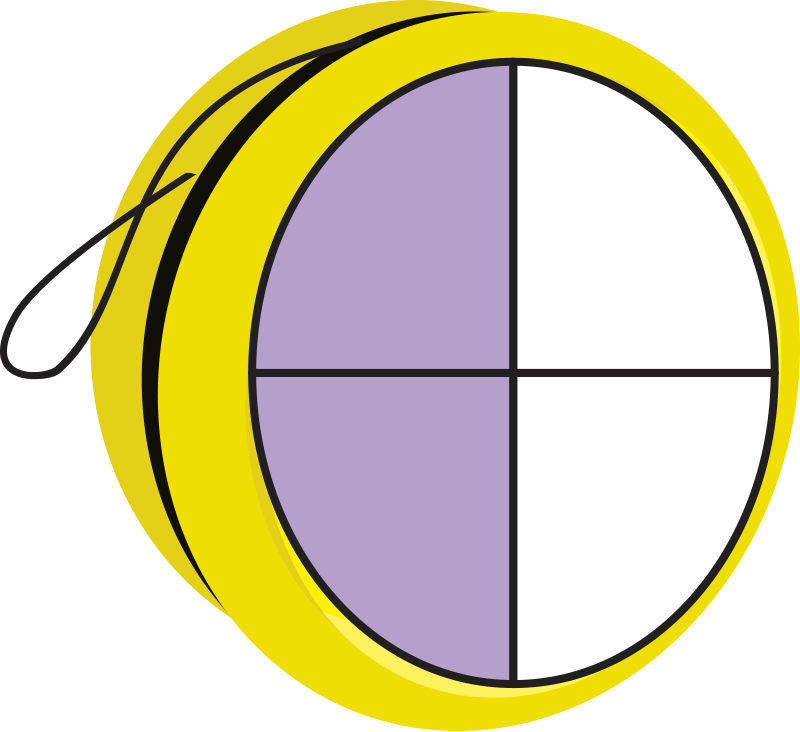
1 of the 4 parts of this ball are colored. Which ball has an equivalent fraction?

Sorry, this fraction is not equivalent because it does not have the same amount of colored area.
Yes! This fraction is equivalent because it shows the same amount of colored area.
Sorry, this fraction is not equivalent because it does not have the same amount of colored area.
Sorry, this fraction is not equivalent because it does not have the same amount of colored area.
Which fraction is equivalent to \({ \frac{2}{2} }\)?

Sorry, that is not correct. These fractions are not equivalent because they name different amounts.
Sorry, that is not correct. These fractions are not equivalent because they name different amounts.
Yes! \({ \frac{8}{8} }\) is equivalent to \({ \frac{2}{2} }\) because they name the same amount.
Sorry, that is not correct. These fractions are not equivalent because they name different amounts.
Which equivalent fractions match this real-life example?
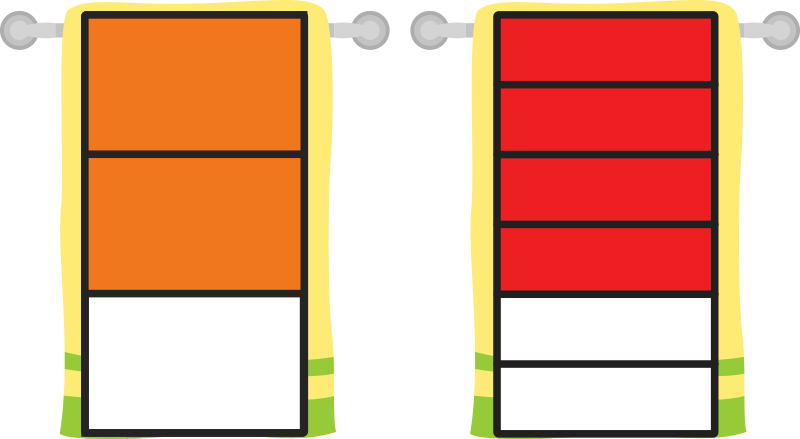
- \({ \frac{2}{3} = \frac{4}{6} }\)
- \({ \frac{0}{6} = \frac{8}{8} }\)
- \({ \frac{2}{3} = \frac{1}{6} }\)
- \({ \frac{1}{4} = \frac{1}{2} }\)
Yes! \({ \frac{2}{3} }\) is equivalent to \({ \frac{4}{6} }\).
Sorry, that is not correct. These fractions show that \({ \frac{2}{3} }\) is equivalent to \({ \frac{4}{6} }\).
Sorry, that is not correct. These fractions show that \({ \frac{2}{3} }\) is equivalent to \({ \frac{4}{6} }\).
Sorry, that is not correct. These fractions show that \({ \frac{2}{3} }\) is equivalent to \({ \frac{4}{6} }\).
4 of the 8 parts of this phone case are colored. Which phone case has an equivalent fraction?

Sorry, this fraction is not equivalent because it does not have the same amount of colored area.
Sorry, this fraction is not equivalent because it does not have the same amount of colored area.
Sorry, this fraction is not equivalent because it does not have the same amount of colored area.
Yes! This fraction is equivalent because it shows the same amount of colored area.
Summary
Questions answered correctly:
Questions answered incorrectly: