Let’s Learn!
How can an input and output table help us find a product?
Goal:
Goal:
Think About It!
Goal: Recognize patterns in an input and output table to help us multiply.
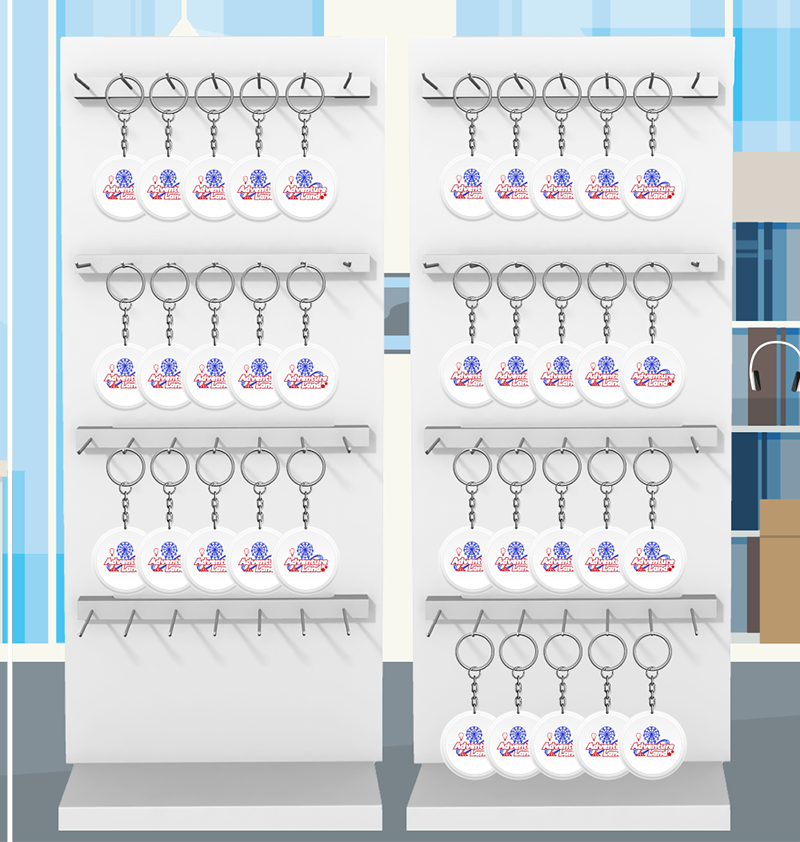
Logan is excited to pick his gift from the gift shop. He wants to look at the key chains! He sees 7 groups of 5 key chains. How many key chains are there in all?
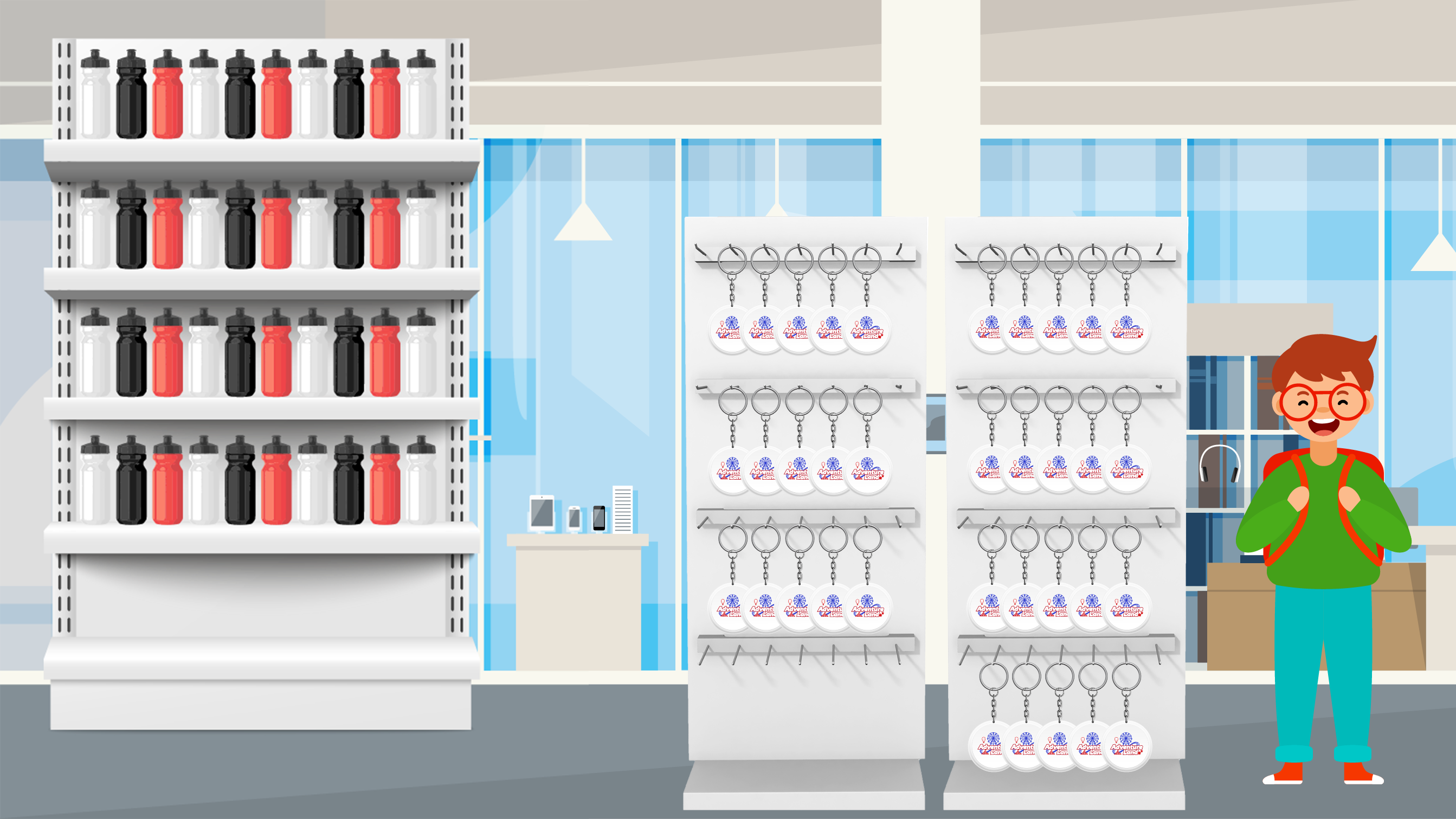
Logan at the gift shop. He sees 7 groups of 5 key chains.
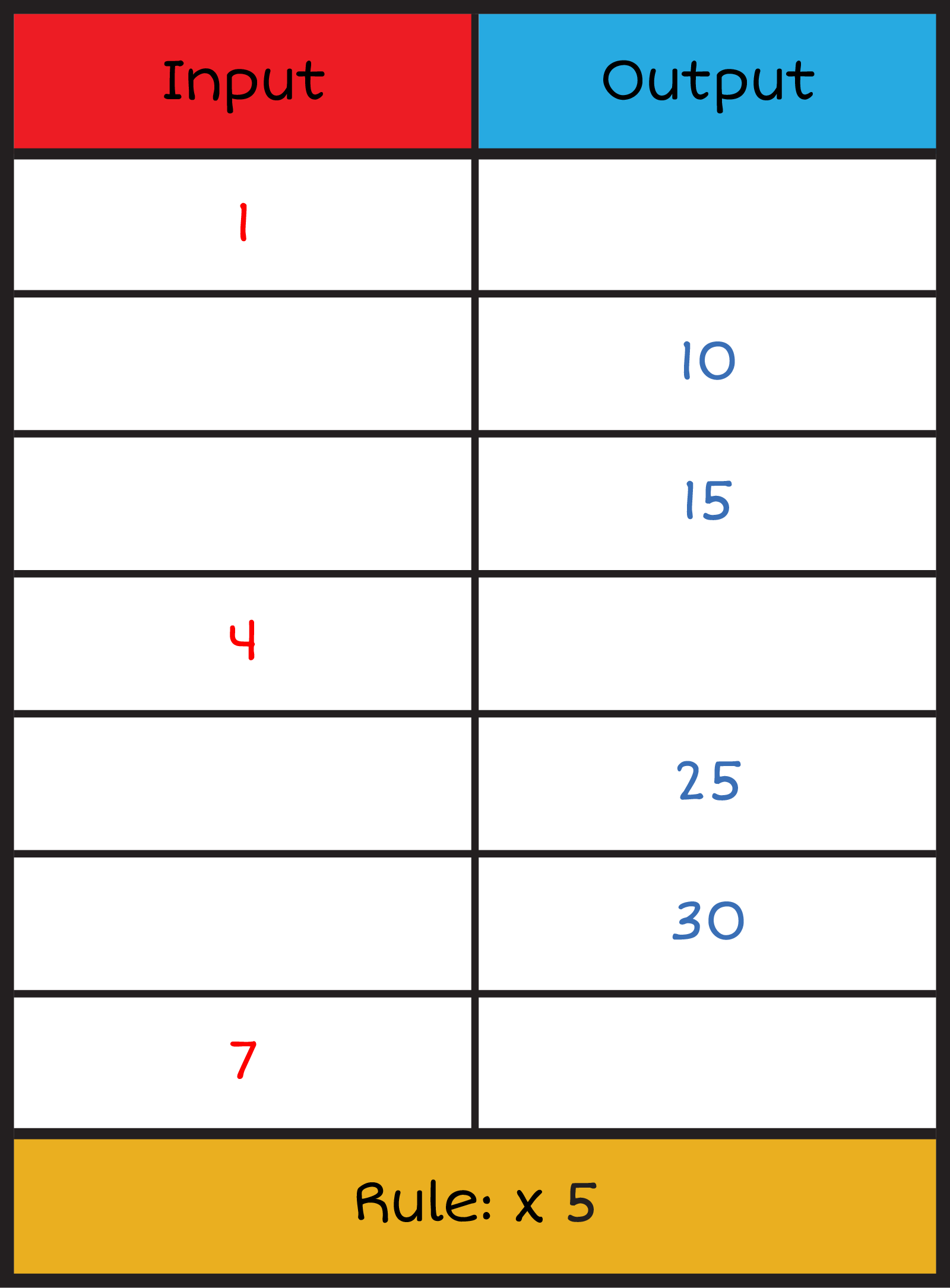
We can use an input and output table to help us find the product! An input and output table (or chart) shows a set of numbers that follow a rule. When an input and output table is vertical, there are input and output columns. When an input and output table is horizontal, there are input and output rows. Numbers go into the input column or row and come out of the output column or row. We put a number into the input column or row. Then we apply the rule: add, subtract, multiply, or divide by a number. Then, the answer goes in the output column or row.
Click the titles in boxes below to see vertical and horizontal input output tables!
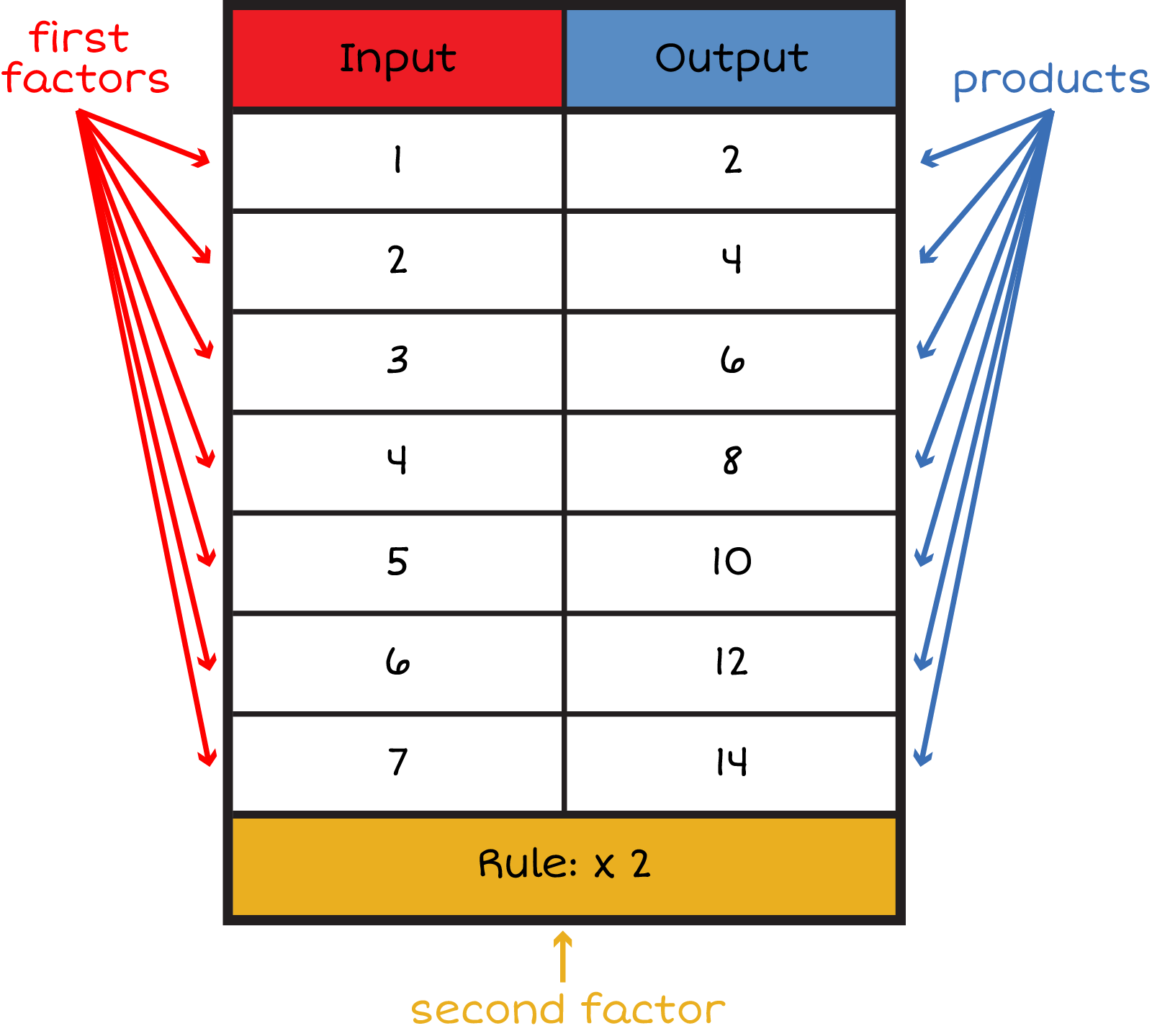
Table header Row, column 1 Input, Column 2 Output
Row 1 Input 1, Output 2
Row 2 Input 2, Output 4
Row 3 Input 3, Output 6
Row 4 Input 4, Output 8
Row 5 Input 5, Output 10
Row 6 Input 6, Output 12
Row 7 Input 7, Output 14
Table Footer, rule: \({\times 2}\)
The first factor are the numbers in the first column
The second factor is the rule \({\times 2}\)
The product are the numbers in the second column
examples of using the table to create the equations row 1\({1 \times 2 = 2}\) row 2 \({2 \times 2 = 4}\)row 3 \({3 \times 2 = 6}\)row 4 \({4 \times 2 = 8}\)row 5 \({5 \times 2 = 10}\)row 6\({6 \times 2 = 12}\) row 7 \({7 \times 2 = 14}\)
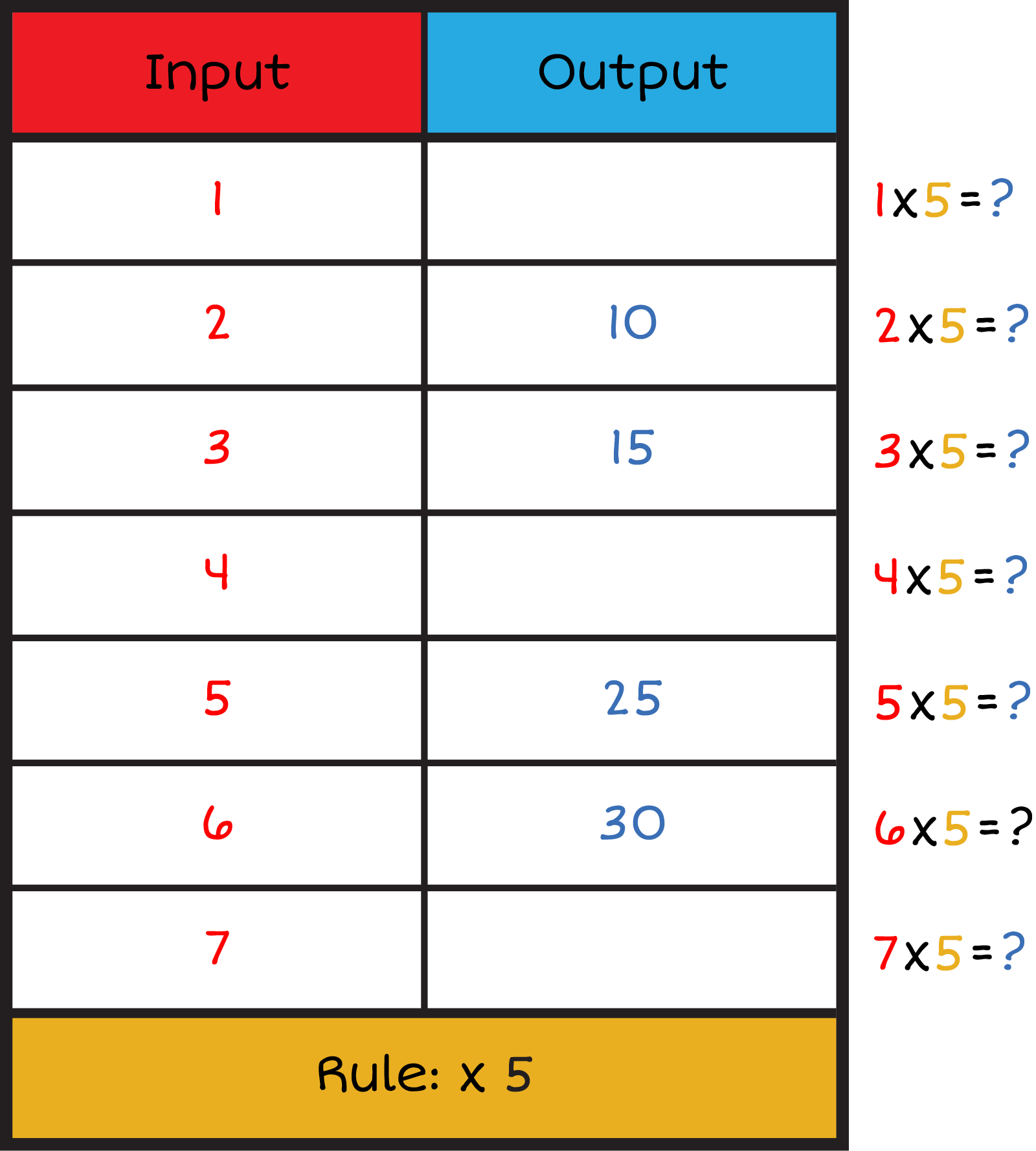
We will use the table as a multiplication strategy! The numbers that go in the input column or row are first factors. Each multiplication sentence has a different first factor. The rule is the second factor. Each multiplication sentence has the same second factor. The numbers that go in the output column or row are the products. They tell us the answer to each multiplication sentence. To fill out an input and output table, we look for the pattern in each column (or row) of the table!
Click each row to see how to fill out a multiplication input and output table!
Column 1, Row 1 Input, Row 2 Output
Row 1, Column 2: 1, the 1 is circled.
Footer Row, Rule: \({\times 3}\)
The input column or row should have numbers that get bigger as you go down the column or to the right along the row. 1 is the first number in this input row, and the numbers will increase by 1. Click Show Me to fill out the rest of the input row!
Column 1, Row 1 Input, Row 2 Output
Row 1, column 2: 1, column 3: 2, Column 4: 3, Column 5: 4, Column 6: 5, Column 7: 6, Column 8: 7
Footer Row, Rule: \({\times 3}\)
Column 1, Row 1 Input, Row 2 Output
Row 1, column 2: 1, column 3: 2, Column 4: 3, Column 5: 4, Column 6: 5, Column 7: 6, Column 8: 7
Footer Row, Rule: \({\times 3}\)
The rule tells you what number you will multiply each input by. This rule is \({\times 3}\). That means you will multiply each input by 3. The input will be the first factor and 3 will be the second factor for each multiplication sentence. Click the Show Me button to see a multiplication sentence for each column using the inputs and the rule!
\({1 \times 3 = ?}\)\({2 \times 3 = ?}\)\({3 \times 3 = ?}\)\({4 \times 3 = ?}\)\({5 \times 3 = ?}\)\({6 \times 3 = ?}\)\({7 \times 3 = ?}\)
Column 1, Row 1 Input, Row 2 Output
Row 1, column 2: 1, column 3: 2, Column 4: 3, Column 5: 4, Column 6: 5, Column 7: 6, Column 8: 7
Footer Row, Rule: \({\times 3}\)
\({1 \times 3 = ?}\)\({2 \times 3 = ?}\)\({3 \times 3 = ?}\)\({4 \times 3 = ?}\)\({5 \times 3 = ?}\)\({6 \times 3 = ?}\)\({7 \times 3 = ?}\)
Column 1, Row 1 Input, Row 2 Output
Row 1, column 2: 1, column 3: 2, Column 4: 3, Column 5: 4, Column 6: 5, Column 7: 6, Column 6: 7
Footer Row, Rule: \({\times 3}\)
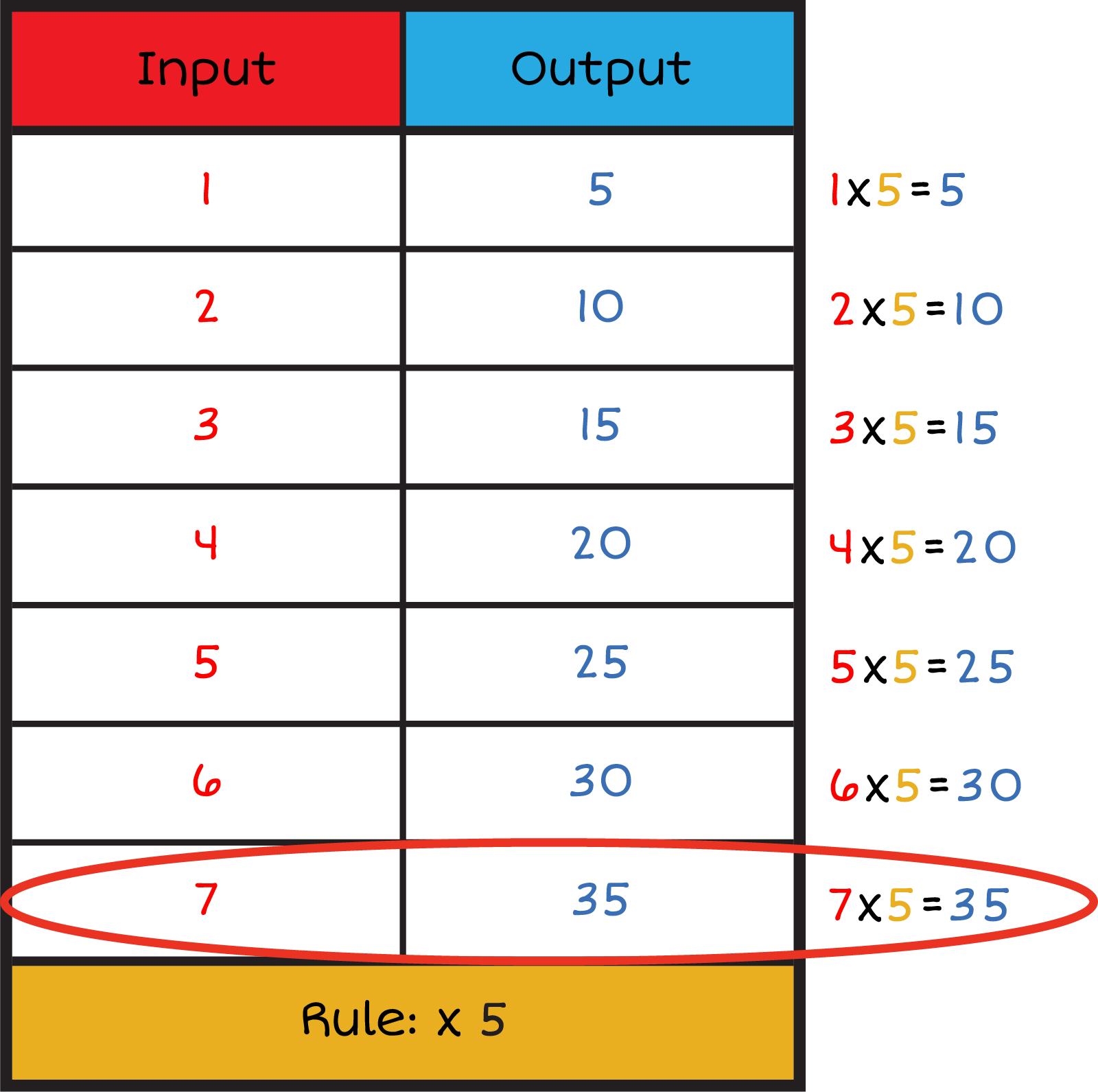
Now we have a multiplication sentence for each column. The product of each sentence is the output! You do not have to write out the multiplication sentences when you do this on your own. You can multiply each input by the rule in your head or skip count by the rule number. You can also add the rule number to each output to get the next output to the right. Click the Show Me button to fill out the output column!
\({1 \times 3 = ?}\)\({2 \times 3 = ?}\)\({3 \times 3 = ?}\)\({4 \times 3 = ?}\)\({5 \times 3 = ?}\)\({6 \times 3 = ?}\)\({7 \times 3 = ?}\)
Column 1, Row 1 Input, Row 2 Output
Row 1, column 2: 1, column 3: 2, Column 4: 3, Column 5: 4, Column 6: 5, Column 7: 6, Column 8: 7
Row 2, column 2: 3, column 3: 6, column 4: 9, column 5: 12, column 6: 15, column 7: 18, column 8: 21
Footer Row, Rule: \({\times 3}\)
Let’s use what we have learned about multiplying with input and output tables to help Logan!
\({7}\)\({\times}\)\({5}\)\({=}\) \({?}\)
Logan sees 7 groups of 5 key chains. That is 7 times 5! We need an input and output table that will help us find the product.
Question
What should be the rule of the input and output table?
\({\times}\)\({5}\) We use the second factor as the rule.
\({7}\)\({\times}\)\({5}\)\({=}\)\({?}\)
Table Header, Row 1, Column 1 Input, Column 2 Output
Row 2, Column 1: 1, Column 2: blank
Row 3, Column 1: blank, Column 2: 10
Row 4, Column 1: blank, Column 2: 15
Row 5, Column 1: 4, Column 2: blank
Row 6, Column 1: blank, Column 2: 25
Row 7, Column 1: blank, Column 2: 30
Row 8, Column 1: 7, Column 2: Blank
Table Rule \({\times 5}\)
Logan has a table that has \({\times}\) \({5}\) as the rule. He filled out some of it, but he needs our help to fill out the rest. Let’s start with the input column. Just like the previous table, the input column will increase by 1 as you go down the column! Click the Show Me button to fill out the input column!
Table Header, Row 1, Column 1 Input, Column 2 Output
Row 2, Column 1: 1, Column 2: blank
Row 3, Column 1: 2, Column 2: 10
Row 4, Column 1: 3, Column 2: 15
Row 5, Column 1: 4, Column 2: blank
Row 6, Column 1: 5, Column 2: 25
Row 7, Column 1: 6, Column 2: 30
Row 8, Column 1: 7, Column 2: Blank
Table Rule \({\times 5}\)
\({7}\)\({\times}\)\({5}\)\({=}\)\({?}\)
Table Header, Row 1, Column 1 Input, Column 2 Output
Row 2, Column 1: 1, Column 2: blank
Row 3, Column 1: 2, Column 2: 10
Row 4, Column 1: 3, Column 2: 15
Row 5, Column 1: 4, Column 2: blank
Row 6, Column 1: 5, Column 2: 25
Row 7, Column 1: 6, Column 2: 30
Row 8, Column 1: 7, Column 2: Blank
Table Rule \({\times 5}\)
We can use the input numbers and the rule to write multiplication sentences for each row. Each input will be the first factor of each multiplication sentence. The rule will be the second factor for all of the multiplication sentences. Click the Show Me button to see!
Table Header, Row 1, Column 1 Input, Column 2 Output
Row 2, Column 1: 1, Column 2: blank \({1 \times 5 = ?}\)
Row 3, Column 1: 2, Column 2: 10 \({2\times 5 = ?}\)
Row 4, Column 1: 3, Column 2: 15 \({3 \times 5 = ?}\)
Row 5, Column 1: 4, Column 2: blank \({4 \times 5 = ?}\)
Row 6, Column 1: 5, Column 2: 25 \({5 \times 5 = ?}\)
Row 7, Column 1: 6, Column 2: 30 \({6 \times 5 = ?}\)
Row 8, Column 1: 7, Column 2: Blank \({7 \times 5 = ?}\)
Table Rule \({\times 5}\)
\({7}\)\({\times}\)\({5}\)\({=}\)\({?}\)
Table Header, Row 1, Column 1 Input, Column 2 Output
Row 2, Column 1: 1, Column 2: blank \({1 \times 5 = ?}\)
Row 3, Column 1: 2, Column 2: 10 \({2\times 5 = 10}\)
Row 4, Column 1: 3, Column 2: 15 \({3 \times 5 = 15}\)
Row 5, Column 1: 4, Column 2: blank \({4 \times 5 = ?}\)
Row 6, Column 1: 5, Column 2: 25 \({5 \times 5 = 25}\)
Row 7, Column 1: 6, Column 2: 30 \({6 \times 5 = 30}\)
Row 8, Column 1: 7, Column 2: Blank \({7 \times 5 = ?}\)
Table Rule \({\times 5}\)
The multiplication sentences we wrote will help us find the outputs, or the products. Some of the outputs are already filled out. Do you notice a pattern? You can skip count by 5's to fill out the rest of the outputs, or you can solve each multiplication sentence. You can also add 5 to an output to get the next output below it. Click the Show Me button to see!
Table Header, Row 1, Column 1 Input, Column 2 Output
Row 2, Column 1: 1, Column 2: 5 \({1 \times 5 = 5}\)
Row 3, Column 1: 2, Column 2: 10 \({2\times 5 = 10}\)
Row 4, Column 1: 3, Column 2: 15 \({3 \times 5 = 15}\)
Row 5, Column 1: 4, Column 2: 20 \({4 \times 5 = 20}\)
Row 6, Column 1: 5, Column 2: 25 \({5 \times 5 = 25}\)
Row 7, Column 1: 6, Column 2: 30 \({6 \times 5 = 30}\)
Row 8, Column 1: 7, Column 2: 35 \({7 \times 5 = 35}\)
Table Rule \({\times 5}\)
Now let's use the table to solve Logan's equation!
Question
What is \({\Large7 \times 5}\)
Table Header, Row 1, Column 1 Input, Column 2 Output
Row 2, Column 1: 1, Column 2: 5 \({1 \times 5 = 5}\)
Row 3, Column 1: 2, Column 2: 10 \({2\times 5 = 10}\)
Row 4, Column 1: 3, Column 2: 15 \({3 \times 5 = 15}\)
Row 5, Column 1: 4, Column 2: 20 \({4 \times 5 = 20}\)
Row 6, Column 1: 5, Column 2: 25 \({5 \times 5 = 25}\)
Row 7, Column 1: 6, Column 2: 30 \({6 \times 5 = 30}\)
Row 8, Column 1: 7, Column 2: 35 \({7 \times 5 = 35}\) This row is circled.
Table Rule \({\times 5}\)
\({7 \times 5 = 35}\). 35 is the output in the row that has 7 as the input. There are 35 key chains in the gift shop!
You can use an input and output table and its patterns to find a product!