Solving Real-World Fraction Problems
How can you apply what you know about fractions to real-world situations?
Goal:
Goal:
There are many real-world situations that will require you to multiply fractions. Work through the problems below to practice multiplying fractions involving real-world scenarios. After you have written your solution to each problem, click the problem to check your work.
Let's use a visual fraction model to show Austin's portion in yellow. First, he is given half the pie. Then, he cuts that half into fourths.
\(\mathsf{ \frac{1}{2} }\) of the pie looks like this:

\(\mathsf{ \frac{1}{4} }\) of \(\mathsf{ \frac{1}{2} }\) the pie looks like this:
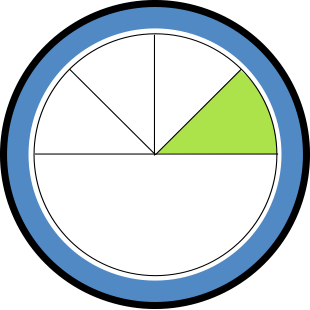
\(\mathsf{ \frac{1}{4} }\) of \(\mathsf{ \frac{1}{2} }\) means \(\mathsf{ \frac{1}{4} \times \frac{1}{2} = \frac{1}{8} }\).
This means that Austin ate \(\mathsf{ \frac{1}{8} }\) of the whole pie.
Bonus: can you figure out what fraction of the pie Austin does not eat?
1 whole pie minus \(\mathsf{ \frac{1}{8} }\) means \(\mathsf{ 1 - \frac{1}{8} }\) which is the same as \(\mathsf{ \frac{8}{8} - \frac{1}{8} = \frac{7}{8} }\). Austin did not eat \(\mathsf{ \frac{7}{8} }\) of the pie.
\(\mathsf{ \frac{2}{3} }\) of each of the 3 wholes equals \(\mathsf{ \frac{6}{3} }\) which, when simplified, equals 2 wholes.

That gives you part of the answer, but what about that \(\mathsf{ \frac{1}{2} }\) acre? Use your knowledge of multiplication of fractions using models to solve for \(\mathsf{ \frac{2}{3} }\) of \(\mathsf{ \frac{1}{2} }\) .
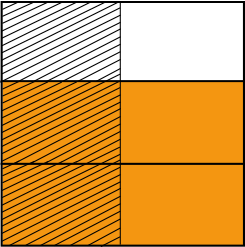
\(\mathsf{ \frac{2}{3} \times \frac{1}{2} = \frac{2}{6} }\) or, when simplified, \(\mathsf{ \frac{1}{3} }\).
This result means that Bryan will need \(\mathsf{ 2\frac{1}{3} }\) acres of land to grow the corn.