Let’s Learn!
What is the commutative property of multiplication?
Goal:
Goal:
Think About It!
Goal: Define the commutative property, and recognize how to use it to solve a multiplication sentence.
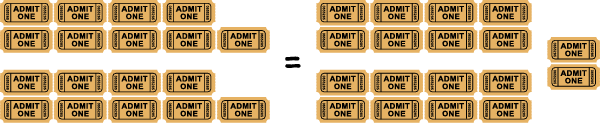
Caleb is helping his teacher count how many tickets the class will need to go on the rides at Adventure Land. There are 3 groups of students who want to go on the roller coaster. There are 6 students in each group. If each student needs 1 ticket to ride the roller coaster, how many tickets does the class need to get? Caleb knows that \({6 \times 3 = 18}\). How can he find the answer to \({3 \times 6 = ?}\)
Caleb at the table in the classroom counting ride tickets. Thre are 18 tickets on the table. Caleb is thinking about the other students. He is thinking about 3 groups of 6 students.
\({6 \times 3 = 18}\) \({3 \times 6 = ?}\)
We can use the commutative property to help Caleb find the answer! The commutative property tells us that the order of the factors in a multiplication sentence does not matter. The product will stay the same! This probably sounds familiar to you. That is because the commutative property can be used for addition or multiplication! It works exactly the same way!
Click each box to see the commutative property for addition and for multiplication!
Did you notice the equations with the sum or the product before the equal sign? They look a bit different, but they are still true! This also works for subtraction and division. This is because the equal sign is there. It tells us that the numbers on the right and the numbers on the left make the same amount. We can switch the order of where the answer and the numbers we are adding, subtracting, multiplying, or dividing go!
|
\({2 + 9 = 11}\) |
\({2 \times 9 = 18}\) |
|
\({11 = 9 + 2}\) |
\({18 = 9 \times 2}\) |
We can use arrays instead of tickets to show the commutative property. An array is a rectangle made up of objects in equal rows and equal columns. Arrays help us see multiplication sentences. We name an array using the number of rows and the number of columns. The first factor is the number of rows. The second factor is the number of columns, or the number of objects in each row. We find the product by counting the total number of shapes in the boxes.
\({2 \times 9 = 18}\)
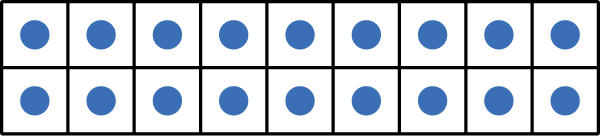
2 rows
9 columns
\({9 \times 2 = 18}\)
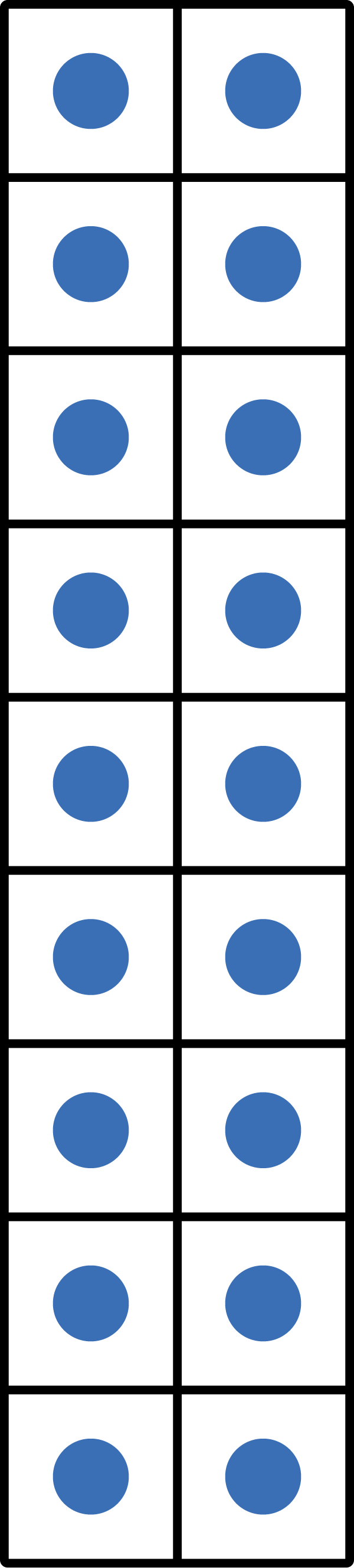
9 rows
2 columns
When we use arrays to show the commutative property, we use the same numbers, but the factors switch places. Look at the arrays for \({2 \times 9}\) and \({9 \times 2}\) above. For the first array, 2 is the number of rows. For the second array, 2 is the number of columns, or the number of items in each row. For the first array, 9 is the number of columns, or the number of items in each row. For the second array, 9 is the number of rows.
Click each row to use an array and the commutative property to solve a multiplication sentence!
\({8 \times 3 = 3 \times 8}\)
\({8 \times 3 = 3 \times 8}\) \({3 \times 8 = 24}\)
If you see the same factors but they are switched, you can use the commutative property! We know \({8 \times 3 = 24}\). That means \({3 \times 8}\) also equals 24!
\({3 \times 8 = 24}\)
How do we know if we are correct? We can check our work using an array! 3 is the first factor and the number of rows. 8 is the second factor and the number of columns. Click the Show Me button to see the array!
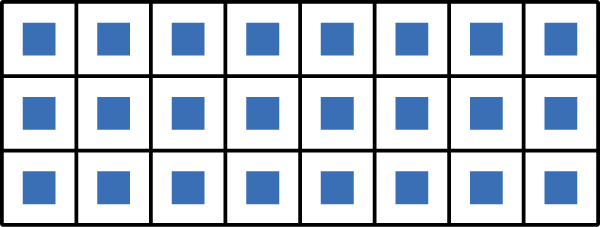
This 3-by-8 array has 24 squares. \({3 \times 8 = 24}\)! We were correct!
Let’s use what we have learned to help Caleb multiply 3 x 6!
|
\({6 \times 3 = 18}\) |
\({3 \times 6 = ?}\) |
Caleb knows that \({6 \times 3 = 18}\). What does \({3 \times 6}\) equal? We can use the commutative property! That is because both equations have 6 and 3 as factors. They switched places!
Question
If \({6 \times 3 = 18}\), what does \({3 \times 6}\) equal?
By the commutative property, \({3 \times 6 = 18}\).
\({3 \times 6 = 18}\)
Did we find the correct product? We need to make an array to find out!
Question
How many rows do we need to make the array?
We need 3 rows to make the array.
Question
How many columns do we need to make the array?
We need 6 columns to make the array.
Now that we know how many rows and columns we need, we can fill each box with a shape. Let’s use triangles! Click the Show Me button to see the array!
There are 18 triangles in the array. We were correct! \({3 \times 6 = 18}\). Caleb’s class needs 18 tickets for the roller coaster!
We can use the commutative property and arrays to solve multiplication sentences!