Ice Skating Fractions
Let’s watch a video about identifying non-unit fractions.
Goal:
Goal:
Madelyn is ice skating! How much of the rink is she skating on? Watch this video to practice identifying non-unit fractions!
It’s New Year’s Eve, and Madelyn is spending a few more hours ice skating before she heads home.
Hey, look at that! Madelyn is skating only on one side of the pond. If we were to partition the pond into 8 equal parts, what fraction of the pond is Madelyn skating on?
Since there are 8 equal parts, the denominator is 8. Madelyn is skating on only 1 . . . 2 parts of the pond, so the numerator is 2. She’s skating on two eighths of the pond!
What if the pond is partitioned into 6 equal parts and Madelyn is skating on 5 parts of it? Do you know what fraction Madelyn is skating on?
The denominator is 6 because there are 6 equal parts in the circle. Do you know the numerator? You got it! 1, 2, 3, 4, 5 parts. The fraction is five sixths because Madelyn is skating on 5 of the sections.
Madelyn is getting cold! It’s almost time for her to go home. Let’s imagine that the pond is divided into three sections and Madelyn is skating on three parts of it. Before she leaves, what fraction of the pond is she skating on now?
Madelyn is skating on three thirds of the circle. Do you know another phrase to use when all parts are shaded, and the numerator and denominator are the same? Yes, one whole! Madelyn is skating on the whole pond. Great job!
You did a great job identifying fractions today! Thanks for helping Madelyn!
Question:
What statement is true about the shaded parts of this partitioned circle?
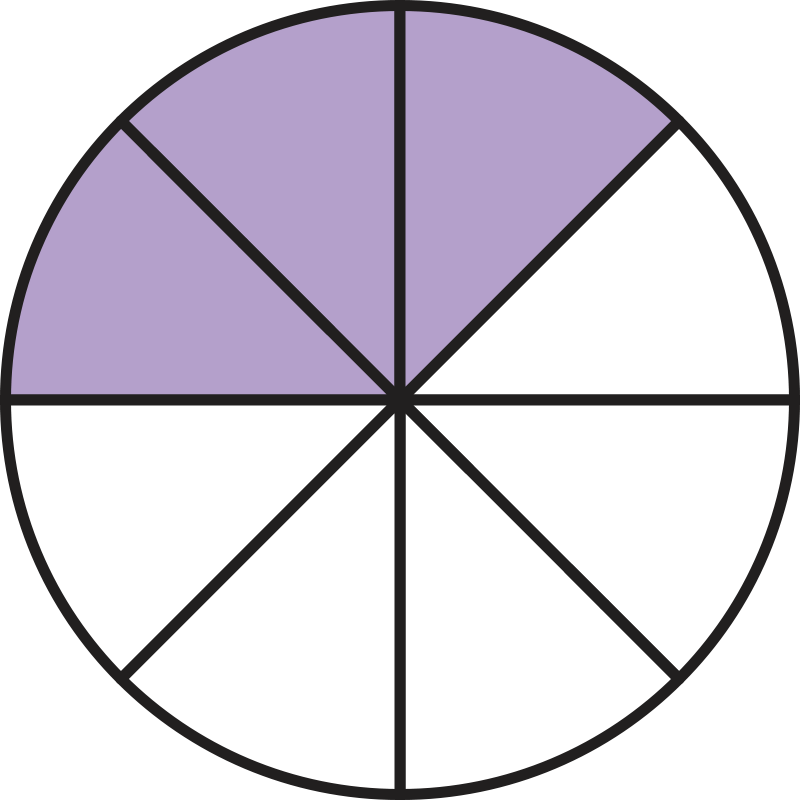
The partitioned circle shows \({ \frac{3}{8} }\) because 3 of the 8 parts are purple.
