Let’s Learn!
How are multiplication and division related?
Goal:
Goal:

Think About It!
Goal: Identify how multiplication and division relate using equal groups.
Zoe, Daniel, Ava, Logan, Madelyn, and Caleb will all participate in some of the snow day activities. When they get to the park, they start different activities with groups of other students. If there are 36 students and 6 groups, how many students are doing each activity?

We need to solve the division sentence 36 \({ \div }\) 6 \({ = }\) ?
Remember, multiplication facts are related to division facts. You can change from a division sentence to a multiplication sentence by moving around the numbers!
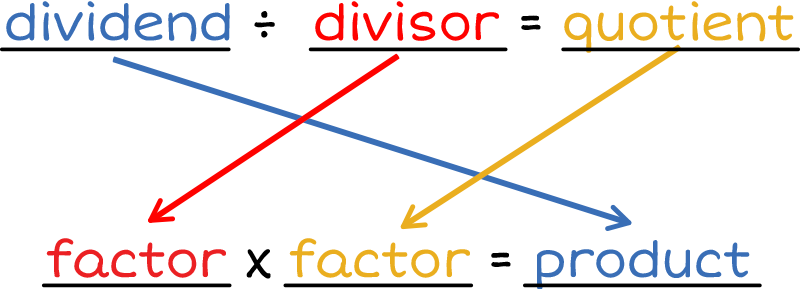
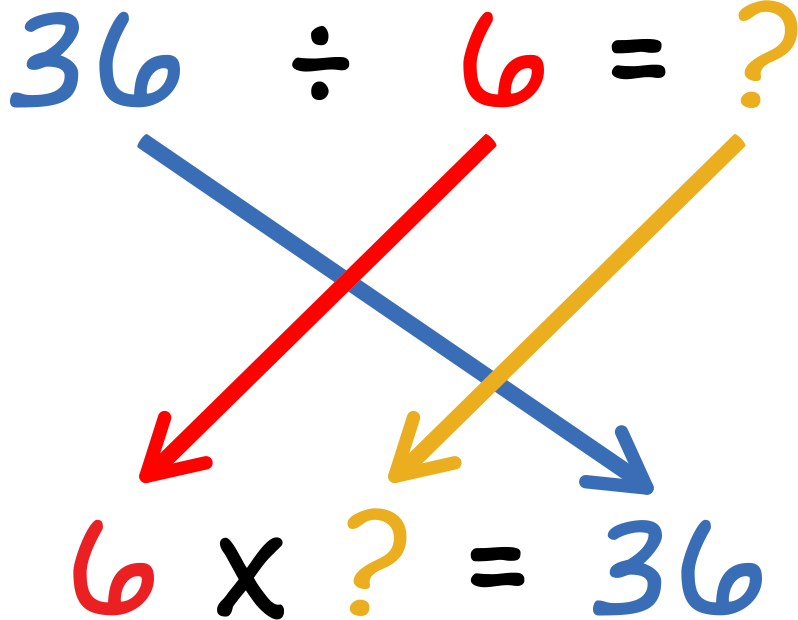
To solve our division problem, we can use one of our division strategies. Do you remember the strategies? Each strategy is shown below. Click the name of the strategy to see how to find the quotient of our division sentence.
| Strategy | Using the Strategy to Solve 36 \({ \div }\) 6 |
|---|---|
|
For arrays or pictures, we organize the total number of students into 6 groups until we run out of students. 
For 36 total students, we get 6 groups of 6 students at each activity. 6 is the quotient. |
|
|
For repeated subtraction, we subtract the divisor from the dividend over and over until we get to zero. The number of times we subtract the repeated subtraction is the quotient. 36 – 6 – 6 – 6 – 6 – 6 – 6 = 0 We have to subtract 6 six times to get to zero. 6 is the quotient. |
|
|
Use a multiplication chart to look at multiplication to solve division. Remember, multiplication and division are opposite operations. Look at the multiplication chart. Find the divisor, 6, on the left-hand side. Then, follow that row to find the dividend, 36. Go up the column from 36, and you will find the quotient, 6! 
36 \({ \div }\) 6 \({ = }\) 6 |
As the students arrive at the park, you will divide them into equal groups. Let’s review our division facts to prepare for the different groups that can be formed.
Let’s look at how many students will be in each group if we have 6 groups of students.
|
Dividend (total number of students) |
Divisor (total number of groups) |
Quotient (number per group) |
Divisor Fact |
|---|---|---|---|
| 6 | 6 | 1 | 6 \({ \div }\) 6 \({ = }\) 1 |
| 12 | 6 | 2 | 12 \({ \div }\) 6 \({ = }\) 2 |
| 18 | 6 | 3 | 18 \({ \div }\) 6 \({ = }\) 3 |
| 24 | 6 | 4 | 24 \({ \div }\) 6 \({ = }\) 4 |
| 30 | 6 | 5 | 30 \({ \div }\) 6 \({ = }\) 5 |
| 36 | 6 | 6 | 36 \({ \div }\) 6 \({ = }\) 6 |
| 42 | 6 | 7 | 42 \({ \div }\) 6 \({ = }\) 7 |
| 48 | 6 | 8 | 48 \({ \div }\) 6 \({ = }\) 8 |
| 54 | 6 | 9 | 54 \({ \div }\) 6 \({ = }\) 9 |
| 60 | 6 | 10 | 60 \({ \div }\) 6 \({ = }\) 10 |
Let’s look at how many students will be in each group if we have 7 groups of students.
|
Dividend (total number of students) |
Divisor (total number of groups) |
Quotient (number per group) |
Divisor Fact |
|---|---|---|---|
| 7 | 7 | 1 | 7 \({ \div }\) 7 \({ = }\) 1 |
| 14 | 7 | 2 | 14 \({ \div }\) 7 \({ = }\) 2 |
| 21 | 7 | 3 | 21 \({ \div }\) 7 \({ = }\) 3 |
| 28 | 7 | 4 | 28 \({ \div }\) 7 \({ = }\) 4 |
| 35 | 7 | 5 | 35 \({ \div }\) 7 \({ = }\) 5 |
| 42 | 7 | 6 | 42 \({ \div }\) 7 \({ = }\) 6 |
| 49 | 7 | 7 | 49 \({ \div }\) 7 \({ = }\) 7 |
| 56 | 7 | 8 | 56 \({ \div }\) 7 \({ = }\) 8 |
| 63 | 7 | 9 | 63 \({ \div }\) 7 \({ = }\) 9 |
| 70 | 7 | 10 | 70 \({ \div }\) 7 \({ = }\) 10 |
Let’s look at how many students will be in each group if we have 8 groups of students.
|
Dividend (total number of students) |
Divisor (total number of groups) |
Quotient (number per group) |
Divisor Fact |
|---|---|---|---|
| 8 | 8 | 1 | 8 \({ \div }\) 8 \({ = }\) 1 |
| 16 | 8 | 2 | 16 \({ \div }\) 8 \({ = }\) 2 |
| 24 | 8 | 3 | 24 \({ \div }\) 8 \({ = }\) 3 |
| 32 | 8 | 4 | 32 \({ \div }\) 8 \({ = }\) 4 |
| 40 | 8 | 5 | 40 \({ \div }\) 8 \({ = }\) 5 |
| 48 | 8 | 6 | 48 \({ \div }\) 8 \({ = }\) 6 |
| 56 | 8 | 7 | 56 \({ \div }\) 8 \({ = }\) 7 |
| 64 | 8 | 8 | 64 \({ \div }\) 8 \({ = }\) 8 |
| 72 | 8 | 9 | 72 \({ \div }\) 8 \({ = }\) 9 |
| 80 | 8 | 10 | 80 \({ \div }\) 8 \({ = }\) 10 |
Let’s look at how many students will be in each group if we have 9 groups of students.
|
Dividend (total number of students) |
Divisor (total number of groups) |
Quotient (number per group) |
Divisor Fact |
|---|---|---|---|
| 9 | 9 | 1 | 9 \({ \div }\) 9 \({ = }\) 1 |
| 18 | 9 | 2 | 18 \({ \div }\) 9 \({ = }\) 2 |
| 27 | 9 | 3 | 27 \({ \div }\) 9 \({ = }\) 3 |
| 36 | 9 | 4 | 36 \({ \div }\) 9 \({ = }\) 4 |
| 45 | 9 | 5 | 45 \({ \div }\) 9 \({ = }\) 5 |
| 54 | 9 | 6 | 54 \({ \div }\) 9 \({ = }\) 6 |
| 63 | 9 | 7 | 63 \({ \div }\) 9 \({ = }\) 7 |
| 72 | 9 | 8 | 72 \({ \div }\) 9 \({ = }\) 8 |
| 81 | 9 | 9 | 81 \({ \div }\) 9 \({ = }\) 9 |
| 90 | 9 | 10 | 90 \({ \div }\) 9 \({ = }\) 10 |
Let’s look at how many students will be in each group if we have 10 groups of students.
|
Dividend (total number of students) |
Divisor (total number of groups) |
Quotient (number per group) |
Divisor Fact |
|---|---|---|---|
| 10 | 10 | 1 | 10 \({ \div }\) 10 \({ = }\) 1 |
| 20 | 10 | 2 | 20 \({ \div }\) 10 \({ = }\) 2 |
| 30 | 10 | 3 | 30 \({ \div }\) 10 \({ = }\) 3 |
| 40 | 10 | 4 | 40 \({ \div }\) 10 \({ = }\) 4 |
| 50 | 10 | 5 | 50 \({ \div }\) 10 \({ = }\) 5 |
| 60 | 10 | 7 | 60 \({ \div }\) 10 \({ = }\) 6 |
| 70 | 10 | 7 | 70 \({ \div }\) 10 \({ = }\) 7 |
| 80 | 10 | 8 | 80 \({ \div }\) 10 \({ = }\) 8 |
| 90 | 10 | 9 | 90 \({ \div }\) 10 \({ = }\) 9 |
| 100 | 10 | 10 | 100 \({ \div }\) 10 \({ = }\) 10 |