Now, it's time for you to try some problems.
Practice 1
Practice 2
The value x is the volume of a metal. The value y is the mass of a metal. Use your calculator to find the correlation coefficient.
| X | 2 | 3 | 5 | 6 | 8 | 9 |
| Y | 5 | 20 | 10 | 15 | 25 | 21 |
Correlation = 0.69

Notice that the points on the graph are fairly spread out. The correlation we calculated is 0.69. If the points were closer to the best-fit line, then the correlation would be closer to 1.0. The correlation +0.69 is positive. The graph shows a positive relationship or correlation.
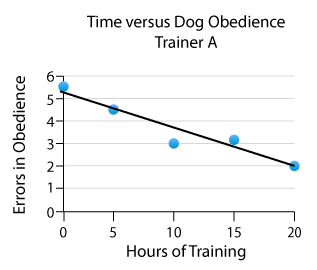
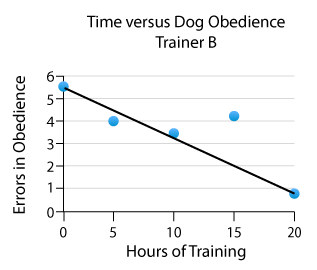
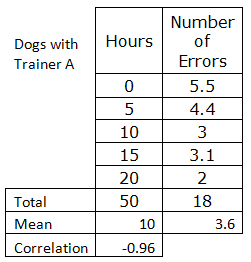
Two dog trainers compared the scores of dogs they had trained in obedience class. Here are the data and scatterplots of the hours of training versus number of errors on the obedience tests. How do you think the correlations will compare. Which set has less variation? Calculate the correlation coefficient using your calculator for data between hours and number of errors for trainer A. Do the same for trainer B. Compare the correlation coefficients.
| Dogs with Trainer A |
Dogs with Trainer B |
|
| Hours | Number of Errors |
Number of Errors |
| 0 | 5.5 | 5.5 |
| 5 | 4.4 | 4 |
| 10 | 3 | 3.5 |
| 15 | 3.1 | 4.2 |
| 20 | 2 | 0.8 |
| 50 | 18 | 18 |
 |
 |
 |
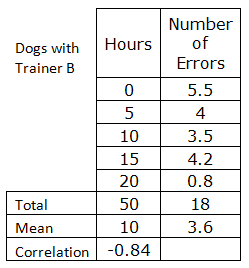 |
Notice that the mean values are the same for both sets of data. The mean value won't always tell you about the amount of variation or spread in the data. As for the correlation coefficients, both show a negative or weak correlation between the number of hours and the errors for the trainers.
