Similar to exponential growth functions, exponential decay functions have both an initial value and a decay factor, but the restrictions on the decay factor are different. Remember that the decay factor represents the rate at which the function decreases.
Exponential Decay Function
\( f(x) = a \cdot b^x \)
a = initial value, \( a \neq 0 \)
b = decay factor, \( 0 < b < 1 \)
x = variable
Let’s walk through an example of creating an exponential decay function and a graph of that function.
For Example
Handan’s parents bought her a car for $16,500 and expect that the car will lose approximately 25% of its value each year. What exponential decay function represents this situation?
The car's purchase price was $16,500. |
This is the initial value. \( a = 16500 \) |
The car loses 25% of its value each year Handan owns it. |
25% represents the decay factor. You must subtract 25% from 100% and convert the answer to a decimal. You can ask yourself, "How much value is left in the car after each year?" \( 100 - 25 = 75% = 0.75 \) |
Use this information to write the function. |
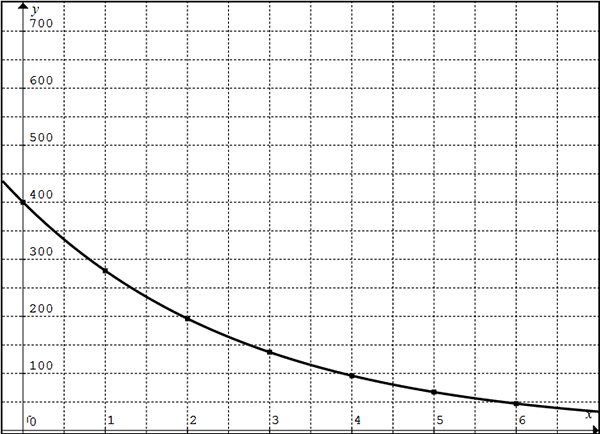
The exponential decay function is \( f(x) = 16,500 \cdot 0.75^x \). |
Create a graph to show how the value of Handan's car decreases over time. You can use the exponential decay function you wrote, \( f(x) = 16,500 \cdot 0.75^x \).
Similar to what you did when creating the graph of exponential growth functions, you can use the function to create a table of values, then plot the points and connect them using a smooth curve.
Create a table of values. |
||||||||||||||
|
||||||||||||||
Plot the points and connect them using a smooth curve. |
||||||||||||||
|
Think you got it?
How well can you write and plot exponential decay functions? Use the activity below to practice. Read the scenario on each tab. Then write the function that describes it, create a table of values, and graph the function on the coordinate plane. Be sure to click each question to check your answer.
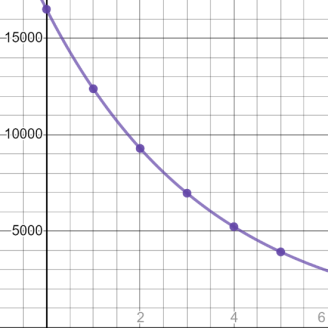
Every year, a high school holds a tennis tournament. The tournament starts with 64 players, and ½ of the players are eliminated after each round.
The initial value is 64 and the decay factor is \( \frac{1}{2} \). The exponential decay function would be:
\( f(x) = 64(\frac{1}{2})^{x} \)
Create a table of values and then plot the points. Connect the points with a solid curved line.
| Number of Rounds |
Players Remaining |
|---|---|
| 0 | 64 |
| 1 | 32 |
| 2 | 16 |
| 3 | 8 |
| 4 | 4 |
| 5 | 2 |
| 6 | 1 |
(Click the graph for a larger view.)
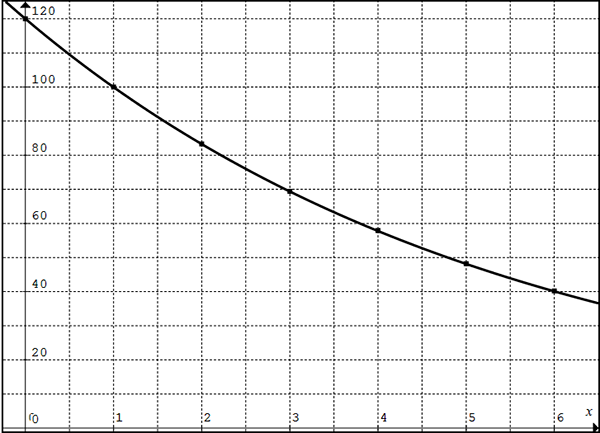
Four years ago, Jack bought a game system for $400. Now he wants to trade in the old system for a new one. If the average depreciation on the game system was 30% each year, how much should he expect to receive when trading in the system?
The initial value is $400 and the decay factor is 0.70. You have to be careful with percents. The decay factor is what is left of the value, rather than how much it decreases. You have to subtract the 30% from 100% and then convert to a decimal.
\( f(x) = 400(0.70)^{x} \)
Create a table of values and then plot the points. Connect the points with a solid curved line.
| Years | Value |
|---|---|
| 0 | $400 |
| 1 | $280 |
| 2 | $196 |
| 3 | $137.20 |
| 4 | $96.04 |
| 5 | $67.23 |
| 6 | $47.06 |
(Click the graph for a larger view.)
Since the game system is four years old, Jack can expect to receive about $96.04 for it.
Angelo is getting better at baking cookies. It took him 120 minutes to make his first batch. Each time he makes them after that, he reduces his time by \( \frac{1}{6} \).
The initial value given is 2 hours and the decay factor is \(\mathsf{ \frac{5}{6} }\). Again, you have to think about the time that is left after the reduction, so he takes \(\mathsf{ \frac{5}{6} }\)th the amount of time each subsequent time he bakes.
\( f(x) = 120(\frac{5}{6})^{x} \)
Create a table of values and then plot the points. Connect the points with a solid curved line.
| Batch Number |
Time to Cook |
|---|---|
| 0 | 120 |
| 1 | 100 |
| 2 | 83.33 |
| 3 | 69.44 |
| 4 | 57.87 |
| 5 | 48.23 |
| 6 | 40.19 |
(Click the graph for a larger view.)
