Now you have all the tools in your tool belt necessary to add two-dimensional vectors. Let's review these tools that you will need to solve the problems below.
Keep in mind that you can only use this problem solving method when you are adding two vectors that are perpendicular to one another. We'll have to apply other techniques to solve other situations at a later time. For now, we will use the Pythagorean Theorem and the tangent function to find the magnitude and direction of a resultant vector.
Right Triangle Information
Pythagorean Theorem
\(\mathsf{ a^{2}}\)+ \(\mathsf{ b^{2}}\) = \(\mathsf{ c^{2}}\)
Trigonometric Relationships
| SOH | CAH | TOA |
|---|---|---|
| \(\mathsf{ \sin{\theta} = \frac{opposite}{hypotenuse}}\) | \(\mathsf{ \cos{\theta} = \frac{adjacent}{hypotenuse}}\) | \(\mathsf{ \tan{\theta} = \frac{opposite}{adjacent}}\) |
Answer each of the following questions in your notes, then click on the answer button to check your work.
The Dog
The Walker
The Golfer

A dog searching for a bone walks 3.50 m south, then 8.20 m at 30.0° north of east. Find the dog's displacement and angle.
| P | 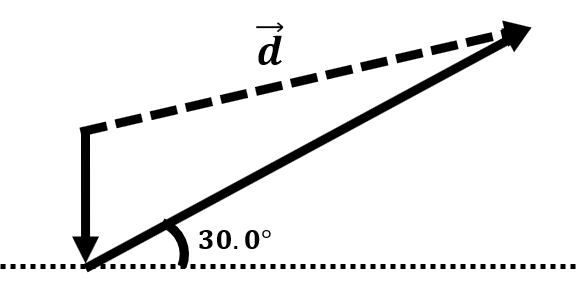 |
| I | \(\small\mathsf{\overrightarrow{d}_1 = 3.50 \text{ m}}\) directly South \(\small\mathsf{\overrightarrow{d}_2 = 8.20 \text{ m}}\) at 30.0° north of east |
| R | \(\mathsf{ \sin{\theta} = \frac{opposite}{hypotenuse}}\) \(\mathsf{ \cos{\theta} = \frac{adjacent}{hypotenuse}}\) \(\small\mathsf{\tan{\theta} = \frac{opposite}{adjacent}}\) \(\small\mathsf{ c^2 = a^2 + b^2 }\) |
| A | \(\small\mathsf{\overrightarrow{d}_{x_1} = (3.50 \text{ m}) (\cos270) = 0.00 \text{ m} }\) \(\small\mathsf{\overrightarrow{d}_{y_1} = (3.50 \text{ m}) (\sin270) = -3.50 \text{ m} }\) \(\small\mathsf{\overrightarrow{d}_{x_2} = (8.20 \text{ m}) (\cos30.0) = 7.10 \text{ m} }\) \(\small\mathsf{\overrightarrow{d}_{y_2} = (8.20 \text{ m}) (\sin30.0) = 4.10 \text{ m} }\) \(\small\mathsf{\overrightarrow{d}_{x} = \overrightarrow{d}_{x_1} + \overrightarrow{d}_{x_2} = 0 \text{ m} + 7.10 \text{ m} = 7.10 \text{ m}}\) \(\small\mathsf{\overrightarrow{d}_{y} = \overrightarrow{d}_{y_1} + \overrightarrow{d}_{y_2} = -3.50 \text{ m} + 4.10 \text{ m} = 0.600 \text{ m} }\) \(\small\mathsf{ c^2 = (7.10 \text{ m})^2 + (0.600 \text{ m})^2 }\) \(\small\mathsf{ c = \sqrt{50.77 \text{ m}^2} = 7.13 \text{ m}}\) \(\small\mathsf{\theta = tan^{-1}(\frac{0.600 \text{ m}}{7.10 \text{ m}}) = 4.83° }\) |
| T | \(\small\mathsf{ \overrightarrow{d} = 7.13 \text{ m}}\) \(\small\mathsf{\theta = 4.83° }\) |
| E | The dog is 7.13 meters from his starting point at an angle of 4.83° north of east. |

A person walks 2.15 m 45.0° north of west, then turns and walks 1.75 m 75.0° north of east. How far and at what angle is this person from their starting point?
| P | 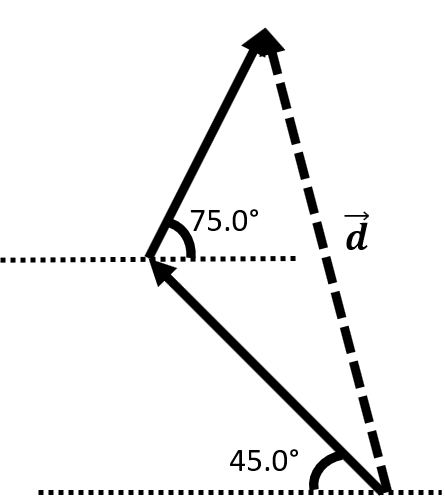 |
| I | \(\small\mathsf{\overrightarrow{d}_1 = 2.15 \text{ m}}\) at 45.0° north of west or 135° \(\small\mathsf{\overrightarrow{d}_2 = 1.75 \text{ m}}\) at 75.0° north of east |
| R | \(\mathsf{ \sin{\theta} = \frac{opposite}{hypotenuse}}\) \(\mathsf{ \cos{\theta} = \frac{adjacent}{hypotenuse}}\) \(\small\mathsf{\tan{\theta} = \frac{opposite}{adjacent}}\) \(\small\mathsf{ c^2 = a^2 + b^2 }\) |
| A | \(\small\mathsf{\overrightarrow{d}_{x_1} = (2.15 \text{ m}) (\cos135) = -1.52 \text{ m} }\) \(\small\mathsf{\overrightarrow{d}_{y_1} = (2.15 \text{ m}) (\sin135) = 1.52 \text{ m} }\) \(\small\mathsf{\overrightarrow{d}_{x_2} = (1.75 \text{ m}) (\cos75.0) = 0.453 \text{ m} }\) \(\small\mathsf{\overrightarrow{d}_{y_2} = (1.75 \text{ m}) (\sin75.0) = 1.69 \text{ m} }\) \(\small\mathsf{\overrightarrow{d}_{x} = \overrightarrow{d}_{x_1} + \overrightarrow{d}_{x_2} = -1.52 \text{ m} + 0.453 \text{ m} = -1.067 \text{ m}}\) \(\small\mathsf{\overrightarrow{d}_{y} = \overrightarrow{d}_{y_1} + \overrightarrow{d}_{y_2} = 1.52 \text{ m} + 1.69 \text{ m} = 3.21 \text{ m} }\) \(\small\mathsf{ c^2 = (-1.067 \text{ m})^2 + (3.21 \text{ m})^2 }\) \(\small\mathsf{ c = \sqrt{9.1656 \text{ m}^2} = 3.38 \text{ m}}\) \(\small\mathsf{\theta = tan^{-1}(\frac{3.21 \text{ m}}{-1.067 \text{ m}}) = -71.6° }\) |
| T | \(\small\mathsf{ \overrightarrow{d} = 3.38 \text{ m}}\) \(\small\mathsf{\theta = -71.6° }\) |
| E | The walker is 3.03 meters at an angle of 71.6° north of west (or 108.4°) away from their starting position. |

A golfer requires three strokes to hit the ball in while he is on the green. During the first putt, the ball rolls 5.0 m due east, the second putt travels 2.1 m at 25.0° north of east. The third putt is 0.75 m due north. What is the resultant and angle needed to put the ball in on one shot?
| P | 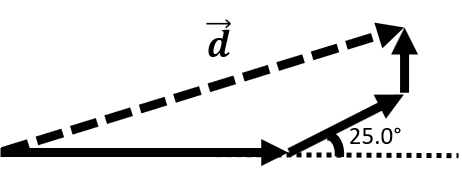 |
| I | \(\small\mathsf{\overrightarrow{d}_1 = 5.0 \text{ m}}\) due east \(\small\mathsf{\overrightarrow{d}_2 = 2.1 \text{ m}}\) at 25.0° north of east |
| R | \(\mathsf{ \sin{\theta} = \frac{opposite}{hypotenuse}}\) \(\mathsf{ \cos{\theta} = \frac{adjacent}{hypotenuse}}\) \(\small\mathsf{\tan{\theta} = \frac{opposite}{adjacent}}\) \(\small\mathsf{ c^2 = a^2 + b^2 }\) |
| A | \(\small\mathsf{\overrightarrow{d}_{x_1} = (5.0 \text{ m}) (\cos0) = 5.0 \text{ m} }\) \(\small\mathsf{\overrightarrow{d}_{y_1} = (5.0 \text{ m}) (\sin0) = 0.0 \text{ m} }\) \(\small\mathsf{\overrightarrow{d}_{x_2} = (2.1 \text{ m}) (\cos25.0) = 1.90 \text{ m} }\) \(\small\mathsf{\overrightarrow{d}_{y_2} = (2.1 \text{ m}) (\sin25.0) = 0.887 \text{ m} }\) \(\small\mathsf{\overrightarrow{d}_{x_3} = (0.75 \text{ m}) (\cos90) = 0.0 \text{ m} }\) \(\small\mathsf{\overrightarrow{d}_{y_4} = (0.75 \text{ m}) (\sin90) = 0.75 \text{ m} }\) \(\small\mathsf{\overrightarrow{d}_{x} = \overrightarrow{d}_{x_1} + \overrightarrow{d}_{x_2} + \overrightarrow{d}_{x_3}= 5.0 \text{ m} + 1.90 \text{ m} + 0.0 \text{ m} = 6.9 \text{ m}}\) \(\small\mathsf{\overrightarrow{d}_{y} = \overrightarrow{d}_{y_1} + \overrightarrow{d}_{y_2} + \overrightarrow{d}_{y_3} = 0.0 \text{ m} + 0.887 \text{ m} + 0.75 \text{ m} = 1.637 \text{ m} }\) \(\small\mathsf{ c^2 = (6.9 \text{ m})^2 + (1.637 \text{ m})^2 }\) \(\small\mathsf{ c = \sqrt{50.2898 \text{ m}^2} = 7.095 \text{ m}}\) \(\small\mathsf{\theta = tan^{-1}(\frac{1.637 \text{ m}}{6.9 \text{ m}}) = 13.344° }\) |
| T | \(\small\mathsf{ \overrightarrow{d} = 7.1 \text{ m}}\) \(\small\mathsf{\theta = 13.3° }\) |
| E | The ball could be hit for 7.1 meters at an angle of 13.3° north of east. |
