The video on the previous page demonstrated a set of steps to use when proving that two triangles are similar. Let's use the example below to review the process.
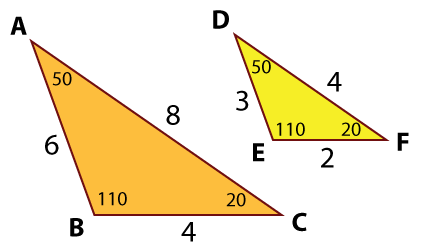
Work through the steps on these slides to see if \(\small\mathsf{ \triangle{ABC} \sim \triangle{DEF} }\) (the symbol \(\small\mathsf{ \sim}\) means "similar to").
Corresponding Angles
First, analyze the triangle and decide if the corresponding angles are congruent. Are the corresponding angles in this set of triangles congruent? In the case of these two triangles, \(\small\mathsf{ \angle{A} \cong \angle{D} }\), \(\small\mathsf{ \angle{B} \cong \angle{E} }\), and \(\small\mathsf{ \angle{C} \cong \angle{F} }\). The first property of similar triangles has been met: All corresponding angles are congruent. Corresponding Sides
Next, check to see if the corresponding sides have a common ratio. What proportions can be written for the corresponding sides of these triangles? \(\mathsf{ \frac{AB}{DE} = \frac{BC}{EF} = \frac{AC}{DF} }\) The second property of similar triangles has been met: The corresponding sides share a common ratio of \(\mathsf{ \frac{2}{1} }\). Are They Similar?
Finally, put steps 1 and 2 together. What conclusion can you draw about these two triangles? Are they similar? Yes. Since the corresponding angles are congruent and the corresponding sides can be written in a common ratio, these two triangles are similar. |



