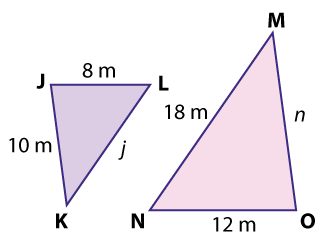In upper-level math courses like this one, you will often need to show something is true by writing special kinds of statements to prove it. In other areas of your life, you make statements about all kinds of things: You may say, "The sky is blue," or "It's raining outside right now." Mathematical statements are sentences that share facts about mathematical relationships. Angle A is congruent to angle B is an example of a mathematical statement. However, when this statement is part of the solution to a geometry problem, it is written this way: \(\small\mathsf{ \angle{A} \cong \angle{B} }\).
Let's work through a problem that requires you to write down mathematical statements about similar triangles.

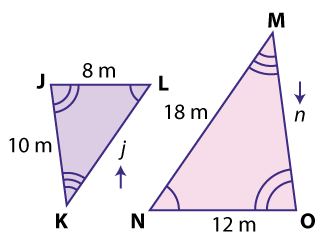
Analyze the triangles above, noting what properties they share and how they seem related. Then use the slideshow below to learn how to write mathematical statements about triangle similarity.
Similar Triangles
The two triangles are similar, but the triangles are flipped over. In your notebook, write a similarity statement for these triangles. Then click the button below to check your answer. \(\mathsf{ \triangle{KLJ} \sim \triangle{MNO} }\) The Angles
If the two triangles are similar, can you write statements about the angles of these two triangles? Write a statement in your notebook. Then click the button to check your answer. If the triangles are similar, then the corresponding angles are congruent. You can write the following statements about the angles: \(\mathsf{ \angle{K} \cong \angle{M} }\) The Sides
If the triangles are similar, can you write statements about the sides? Write some statements about the sides of these triangles. The click the button below to check your work. If the triangles are similar, then corresponding sides can be written as a common ratio. You can write the following proportional statement. \(\mathsf{ \frac{KL}{MN} = \frac{LJ}{NO} = \frac{JK}{OM} }\) Missing Sides
If you know these two triangles are similar, you can find the missing sides j and n. Work the problem in your notebook—then click the button to check your work.
|