The questions on this page are similar to ones you will see on this lesson's quiz. Answer all of these questions, and read the feedback carefully. If you don't understand why one of your answers was incorrect, review that part of this lesson.
True or false: a dilation is the only transformation that produces congruent figures.
- true
- false
False. Since a dilation changes the size of the figure, it produces similar, not congruent, figures.
False. Since a dilation changes the size of the figure, it produces similar, not congruent, figures.
Which of the following is true about similar triangles?
- Corresponding angles are congruent.
- Corresponding sides are in a common ratio.
- All of the above
- None of the above
In order for two triangles to be similar, all corresponding angles must be congruent and all corresponding sides must be in a common ratio.
In order for two triangles to be similar, all corresponding angles must be congruent and all corresponding sides must be in a common ratio.
In order for two triangles to be similar, all corresponding angles must be congruent and all corresponding sides must be in a common ratio.
In order for two triangles to be similar, all corresponding angles must be congruent and all corresponding sides must be in a common ratio.
What similarity property shows that \(\small\mathsf{ \triangle{ABC} \sim \triangle{DEF} }\)?
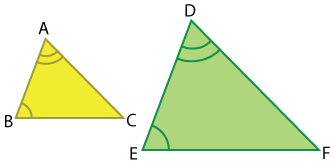
- AA
- SSS
- SAS
- Not enough information
Since two corresponding angles are congruent, these two triangles are similar by the AA similarity property.
Since two corresponding angles are congruent, these two triangles are similar by the AA similarity property.
Since two corresponding angles are congruent, these two triangles are similar by the AA similarity property.
Since two corresponding angles are congruent, these two triangles are similar by the AA similarity property.
What similarity property shows that \(\small\mathsf{ \triangle{ABC} \sim \triangle{KLM} }\)?
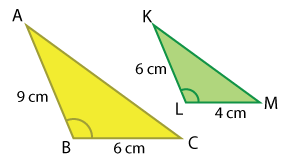
- AA
- SSS
- SAS
- Not enough information
Since two corresponding sides are written in the same ratio and the included corresponding angles are congruent, these two triangles are similar by the SAS similarity property.
Since two corresponding sides are written in the same ratio and the included corresponding angles are congruent, these two triangles are similar by the SAS similarity property.
Since two corresponding sides are written in the same ratio and the included corresponding angles are congruent, these two triangles are similar by the SAS similarity property.
Since two corresponding sides are written in the same ratio and the included corresponding angles are congruent, these two triangles are similar by the SAS similarity property.
True or false: It is enough to know that one set of corresponding angles is congruent in order to show similarity.
- true
- false
In order to show similarity you must know that at least two sets of correspoding angles are congruent.
In order to show similarity you must know that at least two sets of correspoding angles are congruent.
The following two triangles are similar. Find x.
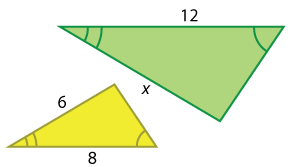
- 10
- 9
- 8
- 7
Set up and solve the following proportion:
\(\small\mathsf{ \frac{8}{12} = \frac{6}{x} }\)
8x = 72
x = 9
Set up and solve the following proportion:
\(\small\mathsf{ \frac{8}{12} = \frac{6}{x} }\)
8x = 72
x = 9
Set up and solve the following proportion:
\(\small\mathsf{ \frac{8}{12} = \frac{6}{x} }\)
8x = 72
x = 9
Set up and solve the following proportion:
\(\small\mathsf{ \frac{8}{12} = \frac{6}{x} }\)
8x = 72
x = 9
Summary
 Questions answered correctly:
Questions answered correctly:
 Questions answered incorrectly:
Questions answered incorrectly:
