When you create a diagram consisting of parallel lines and a transversal, you actually create numerous angles as well. If you analyze your diagram carefully, you'll see that certain types of angles are created by a transversal crossing parallel lines.
The first step for analyzing a diagram containing a transversal is to number the angles.
Click through the tabs below to see the numbers and types of angles created in this specific siutation.
Alternate Interior Angles
Alternate Exterior Angles
Consecutive Interior Angles
Vertical Angles
Corresponding Angles
When a transversal crosses parallel lines, alternate interior angles are equal.
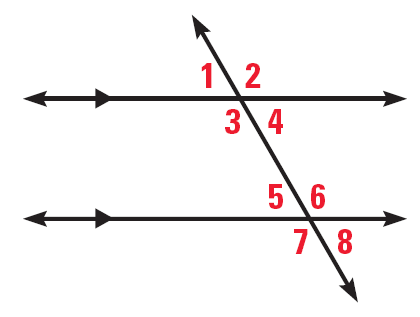
Question
In this diagram, which interior angles are equal in degrees? Write the numbers in your notebook before clicking the button to check your answer.
4 and 5
When a transversal crosses parallel lines, alternate exterior angles are equal.

Question
According to this property, which exterior angles in the diagram are equal in degrees?
2 and 7
When a transversal crosses parallel lines, consecutive interior angles are supplementary.

Question
Do you recall the definition of supplementary angles? How many degrees do supplementary angles add up to?
Question
Which angles in the diagram are supplementary?
2 and 8
3 and 5
4 and 6
When a transversal crosses parallel lines, vertical angles are equal.

Question
According to this property, which pairs of angles in the diagram are equal because they are vertical angles?
2 and 3
5 and 8
6 and 7
When a transversal crosses parallel lines, corresponding angles are equal.

Question
Which pairs of angles in the diagram are equal according to this property?
3 and 7
2 and 6
4 and 8
