As you've read, there are special classifications used to identify angles formed when two lines are cut by a transversal. The video below will walk you through these relationships.
![]() Let's talk about angles formed by a transversal. Now a transversal is simply a line that intersects two or more other lines. Here we've got two examples—Figure A. We've got Line I and Line M, and it's cut, or intersected by, transversal t. Here we've got in Figure B, Line H and Line K intersected by transversal n. Anyway you look at it, we now have eight angles formed when two lines are cut by a transversal. In Figure A, we've got parallel lines; in Figure B they are not parallel because you can see if we were to extend them out, they would intersect eventually. So any two lines can be cut by a transversal and eight angles are going to be formed. There's a special relationship between these eight angles. We can classify these angles specifically.
Let's talk about angles formed by a transversal. Now a transversal is simply a line that intersects two or more other lines. Here we've got two examples—Figure A. We've got Line I and Line M, and it's cut, or intersected by, transversal t. Here we've got in Figure B, Line H and Line K intersected by transversal n. Anyway you look at it, we now have eight angles formed when two lines are cut by a transversal. In Figure A, we've got parallel lines; in Figure B they are not parallel because you can see if we were to extend them out, they would intersect eventually. So any two lines can be cut by a transversal and eight angles are going to be formed. There's a special relationship between these eight angles. We can classify these angles specifically.
Now what I like to do is . . . well, let's go through the different types of angles and then I can show you some ways to remember those.
The first classification are corresponding angles. If something is corresponding, it's in the same position on different intersections. So if you think of the intersection as a box, then the angle in this upper left corner is going to correspond to the angle in this box's upper left corner. So corresponding angles would be Angle 1 and Angle 5. And that holds true the whole way around the box: Angle 2 and Angle 6, Angle 3 and Angle 7, and Angle 4 and Angle 8. Those are all corresponding angles—they are in the same position on the different intersections.
Another type of angle is the alternate interior angles. Now alternate means "on opposite sides"; interior means they're on the inside of the first two lines that were drawn. So this is considered the interior. It's inside the two lines that were drawn. Alternate interior means "opposite sides of the transversal." So let's get rid of the corresponding. So alternate means "opposite sides of the transversal"; interior is between the two original lines. So alternate interior angles would be Angle 3 and Angle 6, and then going the other direction, Angle 4 and Angle 5. Now notice they are alternate because they are not right beside each other. They're kind of diagonal from each other, and they're on opposite sides of the transversal.
Now, another type of angle is the alternate exterior angles. Now I'm sure you can figure out—if this is the interior, out here would be the exterior. They're outside the original two lines. Alternate, again, opposite sides of the transversal. So I've got Angle 1 over here, and I'm going to go across the transversal diagonally, and I come to Angle 8. So Angle 1 and Angle 8 would be alternate exterior. Similarly, Angle 2 and Angle 7 would be the other pair of alternate exterior angles.
And then there's one more type. The final type that we want to talk about are vertical angles. Vertical angles are angles that only share a vertex. So if we look at our diagram, the vertex is this point where the lines intersect. So Angle 1 shares this point only with Angle 4. So Angle 1 and Angle 4 would be considered vertical angles. They are across from each other diagonally, and the only part they share is the vertex in the middle. Similarly, Angle 2 and Angle 3 only share this point in the middle, so they are also vertical angles. And then on the other intersection, we have Angle 5 and Angle 8 and Angle 6 and Angle 7.
Now one thing that you need to keep in mind about these special pairs of angles—when you have parallel lines. When the lines are parallel, these special pairs of angles are congruent or equal: Their measures are equal. So if you have parallel lines cut by a transversal, you know that these pairs of angles listed here are going to be congruent. If the lines are NOT parallel, you cannot say that the angle measures are the same when you're talking about these pairs of angles.
Now what does that do for us? If we know we have parallel lines and we are given the measurement of one of the angles, because of the relationship of these four pairs of angles, we can identify or calculate the measure of all the angles in this figure. So, let's take a look. If Angle 3, for example was 27 degrees, I could fill in all the rest of these angles. First of all, I know that Angle 2 is vertical with angle 3. Vertical angles are congruent. So Angle 2 would also be 27 degrees. Angle 2 and Angle 6 are corresponding angles, so 6 would also be 27 degrees. Angle 2 and Angle 7 are alternate exterior angles, so Angle 7 would also be 27 degrees. Now how do I get 1, 4, 5 and 8? Well, if you look, Angle 1 and Angle 2 form this straight line, so they're supplementary angles. Supplementary angles equal 180 degrees. Angle 2 has already taken up 27 of that 180 degrees, so when you do the calculation, Angle 1 then has to equal 153 degrees because together they have to be 180 degrees. 1 and 4 are vertical angles, so Angle 4 has to be 153 degrees. 4 and 8 are corresponding angles, so 8 has to be 153 degrees. 4 and 5 are alternate interior angles, so 5 also has to be 153 degrees.
This only works if you have parallel lines. These pairs of angles listed here will be congruent.
Practice identifying the relationships between angles cut by a transversal.
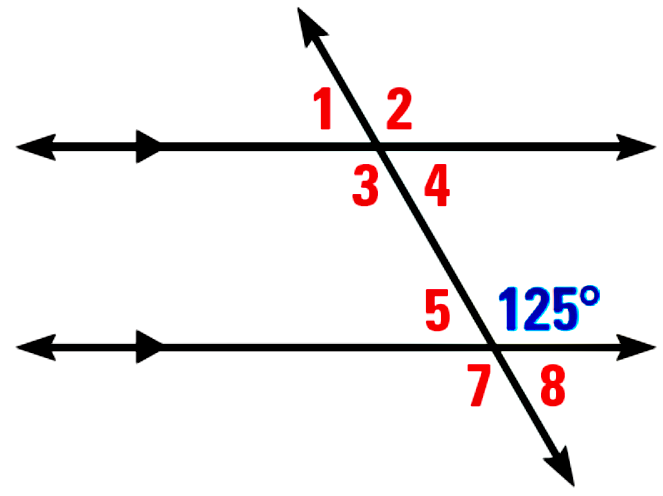
Two horizonal parallel lines, crossed by another line that decreases from left to right. The 8 angles formed by these lines are labeled, from top to bottom and left to right as 1, 2, 3, 4, 5, 125 degrees, 7, 8.
Which angle is equal to 125°?
4
7
2
Angle 2 is a corresponding angle with the angle that is 125°, so it has the same measure.
Angle 2 is a corresponding angle with the angle that is 125°, so it has the same measure.
Angle 2 is a corresponding angle with the angle that is 125°, so it has the same measure.
What is the measure of angle 5?
125°
35°
55°
Angle 5 is supplementary to the angle that is 125°, so they add to 180°. 125°+55°=180°
Angle 5 is supplementary to the angle that is 125°, so they add to 180°. 125°+55°=180°
Angle 5 is supplementary to the angle that is 125°, so they add to 180°. 125°+55°=180°
You got # out of # correct. Click the Retry button for another attempt.
You got a perfect score. Great job!
