125 + (\( x \) + 15) = 180°
Now let's look at a problem involving transversals. To solve this problem, you will need to use what you have learned in this lesson along with your algebra skills.
What is the value of \( x \) in the diagram below?
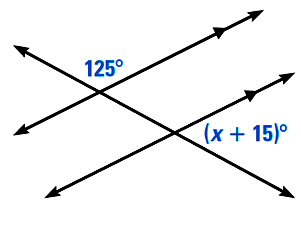
Two parallel lines that increase from left to right, and another line that decreases from left to right and crosses the two parallel lines. The angle formed above the top parallel line and to the right of the other line is marked 125 degrees. The angle formed below the bottom parallel line and to the right of the other line is marked x plus 15 degrees.
Click on the questions below to see how you can arrive at an answer.
| Question to Consider | How to Answer |
|---|---|
| How are the given angles (125° and (\( x \)+15)°) related to each other? | They are both on the outside of the parallel lines (exterior) and on the same side of the transversal (consecutive). The angles are consecutive exterior angles. |
| What angle property can I use to solve for \( x \)? | You can use the fact that consecutive exterior angles formed by a transversal are supplementary. |
| What equation should I set up to find the value of \( x \)? | 125 + (\( x \) + 15) = 180° |
Think about how to solve this equation to find \( x \). Then, place the steps below in the correct order to demonstrate how to solve the equation to find \( x \).
Use the W and S keys to move arrange the items up or down.
\( x \) + (125 + 15) = 180°
\( x \) + 140 = 180°
\( x \) = 180° - 140
\( x \) = 40
Good Job!
