Ohm discovered that there is a relationship between current, resistance, and potential difference in a circuit. Ohm’s Law states that the current (I) in a circuit depends on the difference in electric potential across the circuit (V) and the resistance of the material (R). Specifically, Ohm’s Law states that the current in a circuit is directly proportional to the voltage and inversely proportional to the resistance of the medium through which it flows.
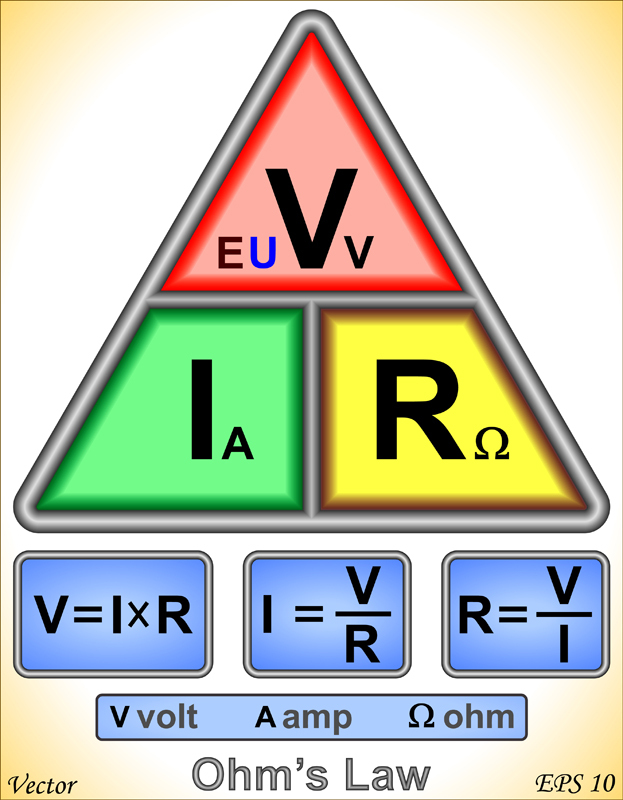
We can use Ohm’s Law to calculate the current in a wire when the resistance and the voltage are known. By solving the equation for the other variables, we can also find the voltage or the resistance if the other two elements are known. Use Ohm's Law to solve each of these problems below. Press the Answer button to check your work.
Example 1
Example 2
Example 3
A 6.0 V battery is connected to a 12.0-Ω resistor. How much current flows through the resistor?
Use Ohm's Law to solve:
\(\mathsf{I = \frac{V}{R} }\)
\(\mathsf{I = \frac{6.0 \text { V}}{12.0 \text { Ω}} }\)
\(\mathsf{I = 0.5 \text { amps} }\)
What is the resistance of the resistor in a circuit that carries 0.625 A of current connected to a 120 V source?
Use Ohm's Law to solve:
\(\mathsf{R = \frac{V}{I} }\)
\(\mathsf{R = \frac{120 \text{ V}}{0.625 \text{ amps}} }\)
\(\mathsf{R = 192 \text{ Ω}}\)
A resistor of 1.0 x 103 Ω is connected to a circuit. The circuit carries 3.0 x 10-3 A of current. What voltage is the power source?
Use Ohm's Law to solve:
\(\mathsf{V = IR }\)
\(\mathsf{V = 3.0 \times 10^{-3} \text{ A} \cdot 1.0 \times 10^3 \text{ Ω} }\)
\(\mathsf{V = 3 \text{ V} }\)
