When working with figures on a coordinate plane, sometimes you can use visual inspection to construct a proof. Other times, you'll definitely need to use algebra. You might have used visual inspection to prove that a figure was a rectangle. Now, try a proof that's a bit more difficult.
Question
Do you remember what operation the diagonals of a rhombus perform on each other?
The diagonals of a rhombus bisect each other.
Consider rhombus WXYZ. Segment XO ≈ 3.54 units. Prove that the diagonals bisect each other.
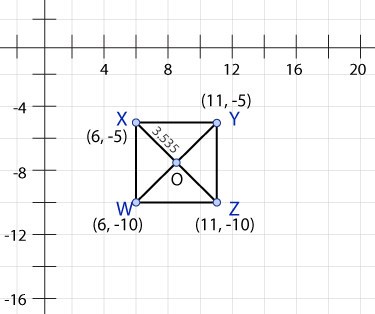
(Because you'll use approximate numbers in the following calculations, your answers won't be exact, but you'll still work through the process used to construct an algebraic proof. Remember, it's most important that you understand the process.)
You can use the properties of a rhombus to prove that the diagonals bisect each other, but in this case, you don't have to. Instead, you can construct an algebraic proof. To do so, read the steps in the table below.
| Mathematically, what does it mean for the diagonals to bisect each other? | WO = OY and XO = OZ. |
| XZ and WY intersect at what angle? | The diagonals of a rhombus are perpendicular to each other. Therefore, they intersect at a right angle. |
| Consider right triangle △XOY. What is the length of XY? | By visual inspection, XY = 5. |
| Now, use the Pythagorean Theorem to calculate the measure of OY. | \(\small\mathsf{ OY = \sqrt {5^2 - 3.54^2} \approx 3.54}\) |
| Next, consider right triangle △YOZ. What is the length of YZ? | By visual inspection, YZ = 5. |
| Use the Pythagorean Theorem to calculate the measure of OZ. | \(\small\mathsf{ OZ = \sqrt {5^2 - 3.54^2} \approx 3.54}\) |
| Finally, consider right triangle △WOZ. What is the length of WZ? | By visual inspection, WZ = 5 |
| Use the Pythagorean Theorem to calculate the measure of OW. | \(\small\mathsf{ OZ = \sqrt {5^2 - 3.54^2} \approx 3.54}\) |
| What do you notice about WO and OOY and about XO and OZ? | WO = OY = 3.54 and XO = OZ = 3.54 |
| What did you prove about the diagonals of a rhombus? | The diagonals of a rhombus bisect each other. |
