At this point, you've developed proofs about special parallelograms--rectangles and rhombuses. Did you know that you can also construct simple algebraic proofs about circles?
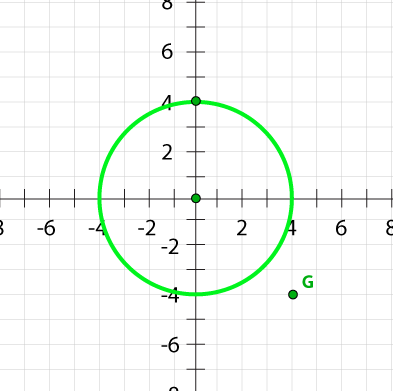
Consider circle P which is centered at the origin (0,0).
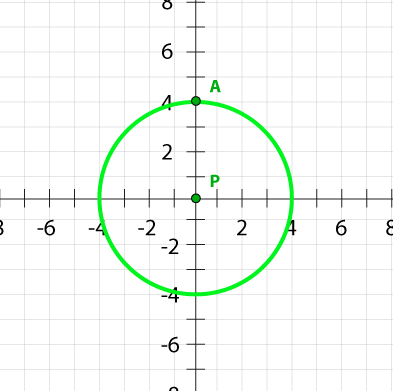
Question
What are the coordinates of point A?
(0,4)
You see that circle P is centered at the origin and contains point (0,4). How can you prove or disprove that any given point lies on the circle? Keep reading to find out.
|
This time, what if instead of seeing the point on the plane, you only know the coordinates of the point. Determine if point (4,0) is on the circle. To make this determination, you could count four units in the +x direction and 0 units in the y direction to see if you land on the circle. Using this method, is (4,0) on the circle? Yes, the point (4,0) lies on the circle.
You could continue to use visual inspection for every given point, and you would most likely get the right answer each time. However, this isn't exactly proof. To construct an accurate proof, you need numbers that verify your conclusions. This time, construct an algebraic proof that either proves or disproves point (3.3, -2.3) lies on the circle. To create your proof, use the steps outlined in the following table.
|
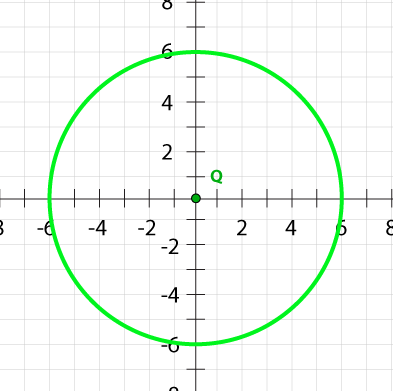
Try constructing your own proof. Consider circle Q centered at the origin. Prove or disprove that point (-3.00, -5.23) lies on the circle. Use the notebook below to construct your proof. The left page contains several questions. Write your answer to each question on the right page in the corresponding line.
Wow, great job!
You got all of them right!
Something's not quite right.
Change any answers with X's and try again.
Question
For any circle centered at the origin, how do you determine if a given point lies on that circle?