You've seen a demonstration of how to construct an algebraic proof that shows the diagonals of a rhombus bisect each other. Next, practice what you learned by creating your own proof.
Given: Parallelogram ABCD is a rhombus.
Prove: △AOB \(\mathsf{ \cong }\) △COD.
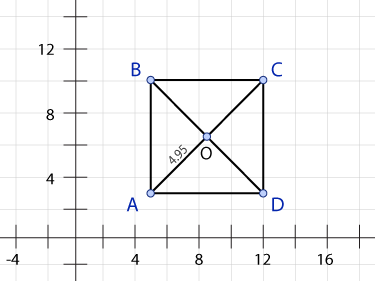
Construct your proof by answering the multiple choice questions that follow.
1. First, you must understand exactly what you need to prove in order to show that △AOB \(\mathsf{ \cong }\) △COD. Which of the following statements is TRUE about congruent triangles?
- Corresponding sides are congruent.
- Corresponding angles are supplementary.
- Adjacent sides are congruent.
- Adjacent angles are complimentary.
Remember the side-side-side (SSS) theorem. If two triangles are congruent, then their corresponding sides are the same length.
Remember the side-side-side (SSS) theorem. If two triangles are congruent, then their corresponding sides are the same length.
Remember the side-side-side (SSS) theorem. If two triangles are congruent, then their corresponding sides are the same length.
Remember the side-side-side (SSS) theorem. If two triangles are congruent, then their corresponding sides are the same length.
2. In order to prove that △AOB \(\mathsf{ \cong }\) △COD, you can show that all three corresponding sides are congruent. By visual inspection, you know AB = CD. What are the other two corresponding sides for which you should show congruency?
- BO = AO and BC = BD
- BO = OD and AO = OC
- CO = OD and AC = BD
- BO = OC and AD = AC
You must show the diagonals bisect each other.
You must show the diagonals bisect each other.
You must show the diagonals bisect each other.
You must show the diagonals bisect each other.
3. What is the length of OD?
- 7.0
- 9.9
- 49.5
- 4.95
OD = \(\mathsf{ \sqrt {7^2 - 4.95^2} }\)
OD = \(\mathsf{ \sqrt {7^2 - 4.95^2} }\)
OD = \(\mathsf{ \sqrt {7^2 - 4.95^2} }\)
OD = \(\mathsf{ \sqrt {7^2 - 4.95^2} }\)
4. What is the length of CO?
- 7.0
- 9.9
- 49.5
- 4.95
OD = \(\mathsf{ \sqrt {7^2 - 4.95^2} }\)
OD = \(\mathsf{ \sqrt {7^2 - 4.95^2} }\)
OD = \(\mathsf{ \sqrt {7^2 - 4.95^2} }\)
OD = \(\mathsf{ \sqrt {7^2 - 4.95^2} }\)
5. What is the length of BO?
- 7.0
- 9.9
- 49.5
- 4.95
OD = \(\mathsf{ \sqrt {7^2 - 4.95^2} }\)
OD = \(\mathsf{ \sqrt {7^2 - 4.95^2} }\)
OD = \(\mathsf{ \sqrt {7^2 - 4.95^2} }\)
OD = \(\mathsf{ \sqrt {7^2 - 4.95^2} }\)
6. Based on the calculations above, which of the following theorems did you prove to show that △AOB \(\mathsf{ \cong }\) △COD.
- side-side-side (SSS)
- angles-side-angle (ASA)
- side-angle-side (SAS)
- angle-angle-angle (AAA)
You proved that the triangles are similar by showing their corresponding sides are congruent.
You proved that the triangles are similar by showing their corresponding sides are congruent.
You proved that the triangles are similar by showing their corresponding sides are congruent.
You proved that the triangles are similar by showing their corresponding sides are congruent.
Summary
Questions answered correctly:
Questions answered incorrectly:
You just used an algebraic proof to show that the diagonals of a rhombus bisect each other. Then, you applied this theorem to show that the inner triangles of a rhombus are congruent. Great job!
