Visual inspection can be quite useful when you consider geometric shapes on a Cartesian coordinate plane. In fact, when you combine that inspection with basic algebra, you can prove or disprove many simple geometric theorems. Until now, you've had to use different properties that justify your proofs. Now, try using the coordinate plane.
Consider figure ABCD defined by four points: (-3,-5) (-10, -7) ( -10, -13) (-3, -10)
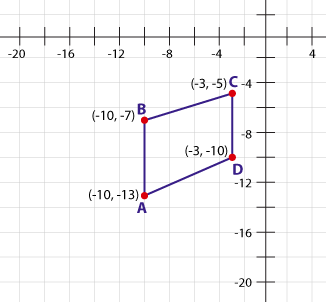
Prove or disprove ABCD is a rectangle.
Use the steps outlined in the table below to complete this algebraic proof.
| Remember the properties of a rectangle. | Rectangles have four right angles, and opposite sides are parallel and congruent. |
| Use the distance formula to calculate the length of the sides. | \(\mathsf{ d = \sqrt {(x_{2} - x_{1} )^2 + (y_{2} - y_{1})^2} }\) |
| What is the length of side BC? | \(\mathsf{ d_{BC} = \sqrt {(-3 - -10)^2 + (-5 - -7)^2} }\) \(\mathsf{ d_{BC} = \sqrt {7^2 + 2^2} }\) \(\mathsf{ d_{BC} = 7.28}\) |
| What is the length of AD? | \(\mathsf{ d_{AD} = \sqrt {(-3 - -10)^2 + (-10 - -13)^2} }\) \(\mathsf{ d_{AD} = \sqrt {7^2 + 3^2} }\) \(\mathsf{ d_{AD} = 7.62}\) |
| If ABCD is a rectangle, what is the relationship between BC and AD? | If ABCD is a rectangle, then \(\mathsf{ BC \cong AD }\). |
| Do your calculations prove or disprove that ABCD is a rectangle? | Since BC = 7.28 but AD = 7.62, the calculations prove that ABCD is NOT a rectangle. |
You just constructed a proof using numbers instead of general properties. You can use algebraic calculations to prove or disprove several other simple geometric theorems and postulates.
