When a figure is placed on a Cartesian coordinate plane, you can write algebraic proofs for many simple geometric theorems and postulates. In fact, throughout this lesson you've constructed several proofs and counter proofs:
- You proved or disproved that a figure defined by four points was a rectangle.
- You proved or disproved that a figure defined by four points was a rhombus.
- You proved the diagonals of a rhombus bisect each other.
- You proved or disproved that a given point lies on a circle centered at the origin.
1. Is this figure defined by points A, B, C, and D a rectangle? Justify your answer.
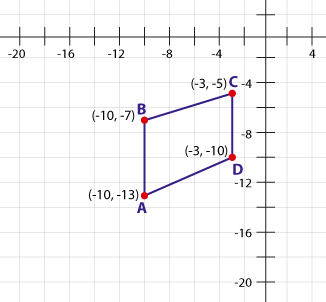
- Yes, ABCD is a rectangle. Based on the coordinates, opposite sides are parallel.
- No, ABCD is NOT a rectangle. Based on the coordinates, line AB is not parallel to line CD.
- No, ABCD is NOT a rectangle. Based on the coordinates, line BC is not parallel to line AD.
- Yes, ABCD is a rectangle. Based on the coordinates, opposite sides are congruent.
A figure is a rectangle if opposite sides are both parallel and congruent. Use the coordinates of each point to see if both conditions are true.
A figure is a rectangle if opposite sides are both parallel and congruent. Use the coordinates of each point to see if both conditions are true.
A figure is a rectangle if opposite sides are both parallel and congruent. Use the coordinates of each point to see if both conditions are true.
A figure is a rectangle if opposite sides are both parallel and congruent. Use the coordinates of each point to see if both conditions are true.
2. What is the length of segment OC?
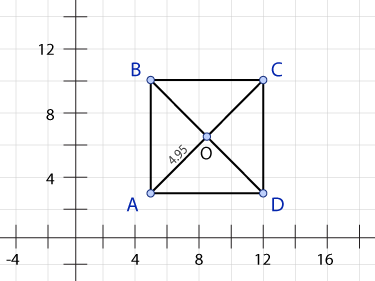
- 4.95
- 7
- 8
- 9.90
The diagonals of a rhombus bisect each other.
The diagonals of a rhombus bisect each other.
The diagonals of a rhombus bisect each other.
The diagonals of a rhombus bisect each other.
3. Circle Q is centered at the origin. If the radius of circle Q is 6, which of the following statements is FALSE?
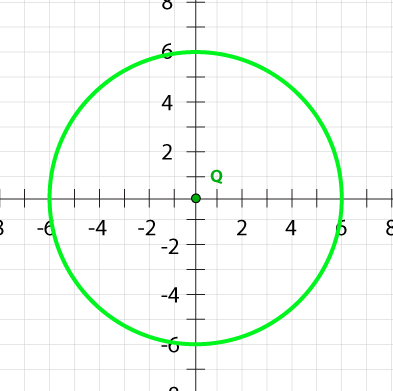
- If the distance from the origin to a given point is 6, then that point lies on circle Q.
- If the distance from the origin to a given point is less than 6, then that point lies inside circle Q.
- If the distance from the origin to a given point is greater than 6, then that point lies outside circle Q.
- If the distance from the origin to a given point is greater than 6, then that point lies on circle Q.
What does the term radius mean? What is the relationship between the radius and points on, inside, and outside the circle?
What does the term radius mean? What is the relationship between the radius and points on, inside, and outside the circle?
What does the term radius mean? What is the relationship between the radius and points on, inside, and outside the circle?
What does the term radius mean? What is the relationship between the radius and points on, inside, and outside the circle?
4. Circle Q is centered at the origin. Is point (3, -6) on the circle? Justify your answer.

- No, because the distance from the origin to point (3, -6) is greater than the radius of the circle.
- No, because the distance from the origin to point (3, -6) is less than the radius of the circle.
- Yes, because the distance from the origin to point (3, -6) is greater than the radius of the circle.
- Yes,because the distance from the origin to point (3, -6) is equal to the radius of the circle.
Find the distance between points (0,0) and (3, -6). Then, compare this distance to the radius of the circle.
Find the distance between points (0,0) and (3, -6). Then, compare this distance to the radius of the circle.
Find the distance between points (0,0) and (3, -6). Then, compare this distance to the radius of the circle.
Find the distance between points (0,0) and (3, -6). Then, compare this distance to the radius of the circle.
Summary
 Questions answered correctly:
Questions answered correctly:
 Questions answered incorrectly:
Questions answered incorrectly:
