Loading...

How do you prove that triangles are congruent?

In the physical world, congruence is used to relate objects to one another according to size and shape. Architects and engineers use their knowledge of congruent triangles to design bridges, houses, skyscrapers, and other structures. If you know how to apply the properties of congruent triangles, you're much more likely to succeed with any construction projects you attempt--as a career or just for fun.

Like other objects, two triangles are congruent when they have the same shape and size. Triangles that are congruent have other properties that are useful to remember as well, so proving that two triangles are congruent is often the first step to solving problems involving objects that seem to be identical in shape and size. Triangles can be proven congruent using one of several methods that involve proving certain corresponding sides and angles congruent.

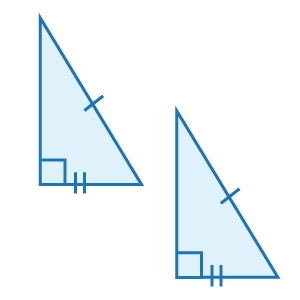
How well do you remember the properties that can be used to prove two triangles are congruent? Each of the diagrams below represents one of those properties. Try to recall the property suggested by each image. Then click the picture to see if you're right.

What does a real-world problem involving triangle congruence look like? Take a look at this one.

XiaZhang Bridge



The XiaZhang Bridge, which was built in 1999 in Fujian, China, and is a whopping 19,442 ft. It's a suspension bridge with two identical triangular structures that appear to be congruent triangles. Suppose the diagram below represents the XiaZhang Bridge. How would you prove that these two parts of the bridge, triangles PKJ and QNL, are congruent? (L is the midpoint of JN)

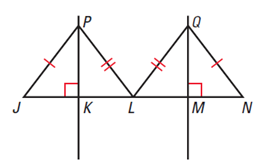
bridge diagram

There are three parts to such a proof. First, you would need to prove that triangles PJL and QNL are congruent. Second, you would to prove that triangle PKL and QML are congruent. Third, you need to show that triangles PKJ and QMN are congruent.

Try writing out the parts of this proof in your notebook. Then check your proof against the sketch below.

Given: 
L is the midpoint of JN. 
PJ is congruent to QN.
PL is congruent to QL
∠PKJ and ∠QMN are right angles.

Prove: \(\mathsf{ \Delta{}}\)PKJ ≅\(\mathsf{ \Delta{}}\)QMN.

Part A: Prove \(\mathsf{ \Delta{}}\)PJL ≅ \(\mathsf{ \Delta{}}\)QNL. 

1) Given: JP ≅ QN
2) Given: PL ≅ LQ
3) Given: L is a midpoint of JN, thus JL ≅ LN
4) So, \(\mathsf{ \Delta{}}\)PJL ≅\(\mathsf{ \Delta{}}\)QLN by SSS.

Part B: Prove \(\mathsf{ \Delta{}}\)PKL ≅\(\mathsf{ \Delta{}}\)QML. 

1) ∠PLK ≅ ∠QLM
2) m∠PKL = m∠QML because they are both right angles.
3) Given: PL ≅ QL
4) So, \(\mathsf{ \Delta{}}\)PKL ≅\(\mathsf{ \Delta{}}\)QML by AAS.

Part C: Prove \(\mathsf{ \Delta{}}\)PKJ ≅\(\mathsf{ \Delta{}}\)QMN.

1) Since L is a midpoint, JL = LN
2) JL – KL = LN – LM by subtraction of line segments
3) JK = MN by substitution
4) So, triangles \(\mathsf{ \Delta{}}\)PKJ ≅\(\mathsf{ \Delta{}}\)QMN by HL.