Try this set of practice questions before you take the graded quiz for this lesson. If you do not do well on this self-check, review the lesson and try again.
What is the measure of the missing angle in this diagram?
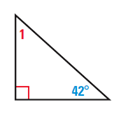
- 90 degrees
- 42 degrees
- 138 degrees
- 48 degrees
Using the Triangle Sum Theorem, the measure of angle 1 = 180 – (42 + 90). So, the measure of angle 1 = 180 – 132 = 48.
Using the Triangle Sum Theorem, the measure of angle 1 = 180 – (42 + 90). So, the measure of angle 1 = 180 – 132 = 48.
Using the Triangle Sum Theorem, the measure of angle 1 = 180 – (42 + 90). So, the measure of angle 1 = 180 – 132 = 48.
Using the Triangle Sum Theorem, the measure of angle 1 = 180 – (42 + 90). So, the measure of angle 1 = 180 – 132 = 48.
Complete the similarity statement for the diagram below using the Leg Rule.
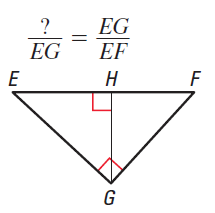
- HF
- EG
- EH
- FG
Since the proportion involves EG as the geometric mean, use the leg rule of geometric means. So, the leg rule states that \(\mathsf{ \frac{EH}{EG} = \frac{EG}{EF} }\) where EH is the segment of the hypotenuse closest to the leg being used as the geometric mean.
Since the proportion involves EG as the geometric mean, use the leg rule of geometric means. So, the leg rule states that \(\mathsf{ \frac{EH}{EG} = \frac{EG}{EF} }\) where EH is the segment of the hypotenuse closest to the leg being used as the geometric mean.
Since the proportion involves EG as the geometric mean, use the leg rule of geometric means. So, the leg rule states that \(\mathsf{ \frac{EH}{EG} = \frac{EG}{EF} }\) where EH is the segment of the hypotenuse closest to the leg being used as the geometric mean.
Since the proportion involves EG as the geometric mean, use the leg rule of geometric means. So, the leg rule states that \(\mathsf{ \frac{EH}{EG} = \frac{EG}{EF} }\) where EH is the segment of the hypotenuse closest to the leg being used as the geometric mean.
How would you prove the triangles in the picture to be congruent?
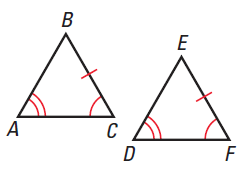
- AAS
- SSA
- SAS
- AAA
The two triangles are congruent by Angle-Angle-Side Congruence Postulate because these corresponding parts are congruent.
The two triangles are congruent by Angle-Angle-Side Congruence Postulate because these corresponding parts are congruent.
The two triangles are congruent by Angle-Angle-Side Congruence Postulate because these corresponding parts are congruent.
The two triangles are congruent by Angle-Angle-Side Congruence Postulate because these corresponding parts are congruent.
In the diagram below, P is a centroid of triangle DEF. What is the length of FH?
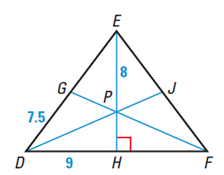
- 9
- 8
- 15.5
- 4.5
Because point P is a centroid, EH is a median that happens to form a right angle. So, this means that DH and HF are congruent. Therefore, FH = DH and so FH = 9.
Because point P is a centroid, EH is a median that happens to form a right angle. So, this means that DH and HF are congruent. Therefore, FH = DH and so FH = 9.
Because point P is a centroid, EH is a median that happens to form a right angle. So, this means that DH and HF are congruent. Therefore, FH = DH and so FH = 9.
Because point P is a centroid, EH is a median that happens to form a right angle. So, this means that DH and HF are congruent. Therefore, FH = DH and so FH = 9.
Summary
Questions answered correctly:
Questions answered incorrectly:
