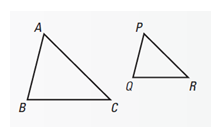
Like congruence, similarity is a way of relating two or more triangles. Similar triangles are proportional, which means they share the same shape, but are not necessarily the same in size. To apply the properties of similarity to a problem, though, you have to make sure that your two triangles are, in fact, similar. Triangles can be proven similar using the SSS (Side-Side-Side) property of similarity: all corresponding pairs of sides are related proportionally. For instance, triangles ABC and PQR would be similar triangles if \(\small\mathsf{ \frac{AB}{PQ} = \frac{BC}{QR} = \frac{CA}{RP} }\).
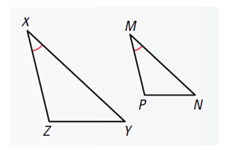
Another way that triangles can be proven similar is through SAS (Side-Angle-Side) similarity—locating two pairs of proportional sides and two corresponding congruent angles that are included between the proportional sides. If you can prove that angles X and M are congruent and that segments XZ and XY exist in the same proportion as segments MP and MN, then you can be sure the two triangles are similar.
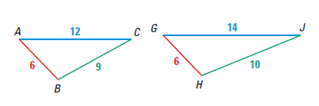
Question
Which property of similar triangles could you use to prove that the two triangles above are NOT similar?
SSS. You have information about the length of all the sides, but the sides do not have the same proportion.
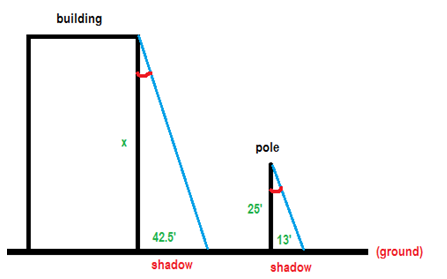
One common application of triangle similarity is determining the height of very tall objects such as skyscrapers. The "shadow method" uses similar triangles and their proportions to calculate the height of tall objects that ordinarily would be very difficult to measure. See if you can picture the scenario below.
On a sunny day, a building casts a shadow that is 42.5' and at the same time, a 25' lamp post casts a shadow that is 13'. What is the height of the building?
Study the slides below to see how you could solve this problem using triangle similarity.
|
Step 1: Sketch a diagram.
Use the information you know to sketch a diagram that includes two triangles with the building and lamp post as one side of each triangle and the structure's shadow as the triangle's base. Step 2: Set up a ratio.
Write a proportion that shows the ratios of corresponding sides of the two triangles. What would the proportion look like that included the ratio of building height to lamp post height and the ration of building shadow length to lamp post shadow length?
\(\mathsf{ \frac{\text{height of the building}}{\text{height of the lamp post}} = \frac{\text{shadow of the building}}{\text{shadow of the lamp post}} }\)
\(\mathsf{ \frac{x}{25} = \frac{42.5}{13} }\) Step 3: Solve the proportion for the height of the building.
\(\mathsf{ \frac{x}{25} = \frac{42.5}{13} }\) Solve the proportion in your notebook. Then check your work.
|
 |
