In a geometry course, you may be given a triangle or a description of one and asked to "solve for" the triangle's missing parts--to determine the length of a side, for instance, or the measure of an angle. In life outside the classroom, though, you are not given that kind of information so neatly. You have to learn how to recognize situations that might be resolved by first imagining or drawing a triangle, and then figuring out its missing parts.
The Triangle Sum Theorem is the most common approach used to solve these kinds of problems.
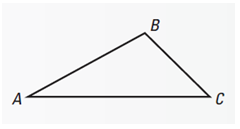Triangle Sum Theorem: All of the angle measures inside of a triangle sum, or add up, to 180 degrees. For the given triangle ABC, m∠A + m∠B + m∠C = 180 degrees.
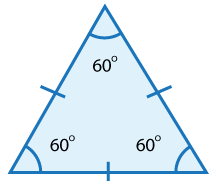
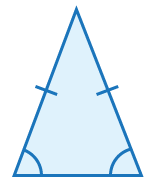
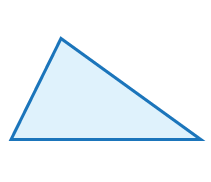
To apply this theorem successfully, though, it helps to recall the various types of triangles-- equilateral, isosceles and scalene--and their properties. See how well you remember this information; for each triangle below, decide which type of triangle it is and recall its main properties. Then click the image to check your memory.
Now try applying the Triangle Sum Theorem to a typical geometry problem:
Find the measure of angles 1, 2, and 3 in the triangles below.
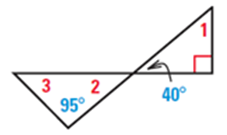
Question
Solve this problem in your notebook. Then click the button to check your work.
Angle 1 is 180 – (90 + 40) = 180 – 130 = 50 degrees.
Angle 2 is a vertical angle and so is equal to 40 degrees.
Angle 3 is 180 – (95 + 40) = 180 – 135 = 45 degrees.
Try the next problem on your own by completing each tab.
Suppose you are making a clothing hanger from a wire. The total amount of the wire is 86 cm. You need 20 cm to make the hook part of the hanger. The triangle part of the hanger is an isosceles triangle (two sides are equal in length). The length of a side is \(\small\mathsf{ \frac{3}{5} }\) times the length of the base. What are the dimensions of the triangular part of the hanger?
Step 1
Step 2
Step 3
Step 4
Step 1: Amount of wire to use
Question
How much wire is needed for the triangular part?
The amount of wire for the triangular part of the hanger is 86cm – 20cm = 66cm.
Step 2: Figure out the base and legs
We do not know the base and legs of the triangular part of the hanger. But, we know that the legs are \(\small\mathsf{ \frac{3}{5} }\) times the base. So, Let x = the base of the triangle.
Question
If one leg is \(\small\mathsf{ \frac{3}{5} }\) of the base, then one leg is \(\small\mathsf{ \frac{3}{5} }\)x. What is the other leg? Why?
Since it is an isosceles triangle, two of the sides or legs are congruent, so the other leg is also \(\small\mathsf{ \frac{3}{5} }\)x.
Step 3: Putting it all together
All sides of the triangular part of the hanger should add up to 66.
Question
What equation can be used to represent the sum of all the sides of the triangular part of the hanger?
\(\small\mathsf{ \frac{3}{5} }\)x + \(\small\mathsf{ \frac{3}{5} }\)x + x = 66
Step 4: Solving the Equation
Question
What is x (base of the hanger) in the equation, \(\small\mathsf{ \frac{3}{5} }\)x + \(\small\mathsf{ \frac{3}{5} }\)x + x = 66?
\(\small\mathsf{ \frac{6}{5} }\)x + x = 66
\(\small\mathsf{ \frac{11}{5} }\)x = 66
x = 30 cm.
Question
What measure are the two legs of the hanger?
The legs of the triangle are \(\small\mathsf{ \frac{3}{5} }\)x. So, they are both \(\small\mathsf{ \frac{3}{5} }\)(30) = 18 cm.
