In exponential growth, an investment or population grows as time passes. This is different than exponential decay, in which the value of a purchase, the amount of radiation coming from radioactive materials, or the number of people infected with a virus decreases as time passes.
The general form of the function for exponential decay is the same as the general form of the function for exponential growth, but the terms a and b have different restrictions. Watch the video below to learn these differences and to see how to plot an exponential decay curve on the xy-plane.
As you watch this video, use the study guide to follow along if you'd like. Click the button below to download the study guide.
Recently you learned about exponential growth functions. These functions were written as \( f(x)=a \cdot b^x \) where “a” represents the initial value of the function, and “b” represents the growth factor. And we noted that exponential growth functions won’t have an “a” value equal to zero, and the “b” value will be any number larger than one.
Did you stop to think about why we have these restrictions? Well, if “a” were to equal zero, then it multiplied by the rest of the function, would always equal zero. This wouldn’t be very interesting. Now, if “b” were less than one, then our growth factor wouldn’t allow our function to grow at all. Think about it – if a stack of pennies grows by a half each hour, wouldn’t it actually be getting smaller? This is exactly what the phrase “exponential decay” describes.
In an exponential decay function, not only is the “b” value less than 1, but is also greater than zero. Meanwhile “a” is not permitted to be zero. If you think about these restrictions, they should make sense. If “b” was one, then “a” times one to any power is always “a” and this isn’t very interesting to us. Again if “b” was zero, then it raised to a power and multiplied by the rest of the function would always equal zero – not very interesting. If “b” was a negative number, we would encounter some interesting results, but they’d be very difficult to interpret. If “a” equals one, for negative “b” values, an even-number exponent would return a positive result, and an odd-number exponent would return a negative result. Non-integer exponents would produce some negative results, but also some results would return as a non-real-number result. Because of all of these differences, we restrict our “b” value to be greater than zero.
Try graphing the following exponential decay by first creating a table of data, then plotting the coordinates. Pause the video and resume playback to check your work… Notice that it was necessary to adjust the scale in order to fit these coordinates in the supplied coordinate system. And I just realized I reversed the order of the x-coordinates. Let me fix this graph… Now this is an exponential decay.
To finish this video, I would like to provide a few examples of exponential expressions. I’d like for you to simply evaluate each by following the order of operations. You may use a calculator to simplify each step, but please try not to evaluate the expression all at once. Pause the video now, and resume playback to see my solutions.
Which is the general form of an exponential decay function?
- \( f\left( x \right) = b \cdot a^{x} \)
- \( f\left( x \right) = a^{b} \)
- \( f\left( x \right) = a \cdot b^{x} \)
An exponential decay function has the form \( f\left( x \right) = a \cdot b^{x} \).
An exponential decay function has the form \( f\left( x \right) = a \cdot b^{x} \).
An exponential decay function has the form \( f\left( x \right) = a \cdot b^{x} \).
What happens to an exponential decay function if the value of a = 0?
- When a = 0, the entire function is equal to 0.
- When a = 0, the function becomes a growth function.
- When a = 0, the function becomes quadratic.
Substitute a = 0 into the general form of the exponential decay function, \( f\left( x \right) = a \cdot b^{x} \), to see what happens.
Substitute a = 0 into the general form of the exponential decay function, \( f\left( x \right) = a \cdot b^{x} \), to see what happens.
Substitute a = 0 into the general form of the exponential decay function, \( f\left( x \right) = a \cdot b^{x} \), to see what happens.
What restriction is placed on the value of b for functions that represent exponential decay?
- \( - 1 < b < 0 \)
- \( 0 < b < 1 \)
- \( - 1 < b < 1 \)
Functions that represent exponential decay have restrictions of \( 0 < b < 1 \).
Functions that represent exponential decay have restrictions of \( 0 < b < 1 \).
Functions that represent exponential decay have restrictions of \( 0 < b < 1 \).
Does the graph below represent exponential decay? Explain.
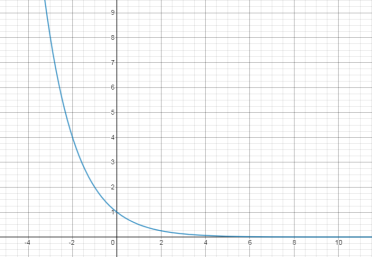

- Yes because the x-values increase as you read the graph from left to right.
- Yes, because the y-values decrease as you read the graph from left to right.
- Yes, because the domain of the function is all real numbers.
Graphs that represent exponential decay decrease as you read them from left to right.
Graphs that represent exponential decay decrease as you read them from left to right.
Graphs that represent exponential decay decrease as you read them from left to right.
Summary
Questions answered correctly:
Questions answered incorrectly:
