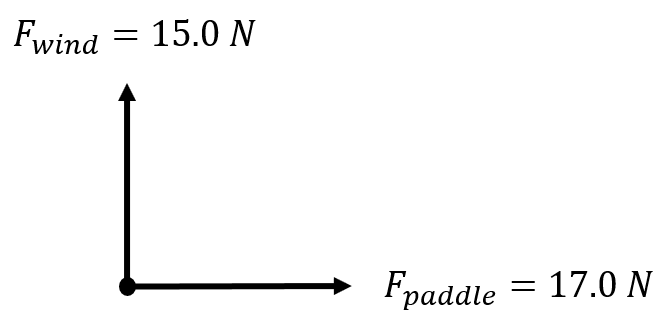
Consider this problem: A woman is standing on a paddle board (mass of woman and paddle board is 1300.0 kg). By paddling, she causes an average force of 17.0 N to be applied to the raft in the direction due east. The wind also exerts a force on the raft. This force has a magnitude of 15.0 N and points due north. Ignoring any resistance from the water, find the raft's acceleration and angle of travel. This is a situation where you have to find the net force prior to working with Newton's Second Law. Click through the slideshow below to work through the steps for this problem.
 Finding Net Force
Finding Net Force
In the Net Force & Newton's First Law lesson, you studied how to find net force using free-body diagrams. You can review that material for more help.
|
Draw a Free-body Diagram It is important in all problems dealing with forces to draw a free-body diagram. This not only helps you determine what is given, but it will help you figure out the answer as well.
List All the Given Information \(\small\mathsf{ \overrightarrow{F_{applied}} = 17.0 \text{ N} }\), east Determine the Equations \(\small\mathsf{ \overrightarrow{F_{net}} = \sum \overrightarrow{F} }\) Find the Net Force Since the two forces are at right angles to one another, add them tip to tail (creating a right triangle). Magnitude: Use the Net Force in Newton's Second Law Equation \(\small\mathsf{ \overrightarrow{F} = m \overrightarrow{a} }\) |
Question
The angle for the acceleration is in the same direction as the net force. Is this always the case?
Yes! The acceleration will always be in the direction of the net force.