Let's practice this process a couple times before we move on. Work through each of the problems below and check your work.
| Problem | Picture | Given/Find | Equation | Solution |
|---|---|---|---|---|
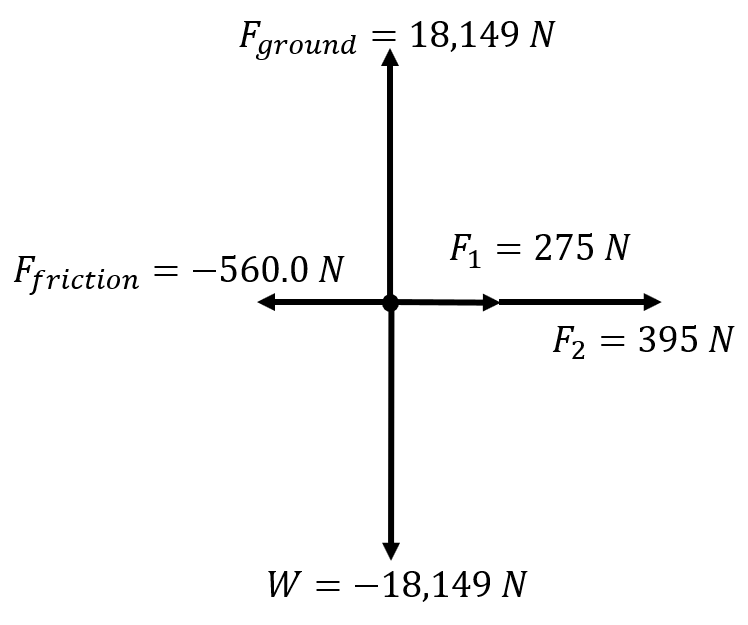
| Two people are pushing a stalled car that has a mass of 1850 kg. One person applies a force of 275 N to the car, while the other person applies 395 N, in the same direction. A third force of 560.0 N (friction) acts opposite these forces. Find the accleration of the car. |
|
\(\small\mathsf{ \overrightarrow{F}_{1-applied} = 275 \text{ N} }\) \(\small\mathsf{ \overrightarrow{F}_{2-applied} = 395 \text{ N} }\) \(\small\mathsf{ \overrightarrow{F}_{friction} = -560.0 \text{ N} }\) \(\small\mathsf{ \overrightarrow{F}_{net} = ? \text{ N} }\) \(\small\mathsf{ \overrightarrow{a} = ? \text{ m/s}^2 }\) \(\small\mathsf{ m = 1850 \text{ kg} }\) |
\(\small\mathsf{ \overrightarrow{F}_{net} = \sum \overrightarrow{F} }\) \(\small\mathsf{ \overrightarrow{F} = m \overrightarrow{a} }\) |
Find the net force: \(\small\mathsf{ \overrightarrow{F_{net}} = \overrightarrow{F}_{1-applied} + \overrightarrow{F}_{2-applied} + \overrightarrow{F}_{friction} }\) \(\small\mathsf{ \overrightarrow{F}_{net} = 275 \text{ N} + 395 \text{ N} + -560.0 \text{ N} }\) \(\small\mathsf{ \overrightarrow{F}_{net} = 110. \text{ N} }\) Find the acceleration: \(\small\mathsf{ 110. \text{ N} = (1850 \text{ kg}) \overrightarrow{a} }\) \(\small\mathsf{ \overrightarrow{a} = \frac{110. \text{ N} }{1850 \text{ kg}} }\) \(\small\mathsf{ \overrightarrow{a} = 0.0595 \text{ m/s}^2 }\) |
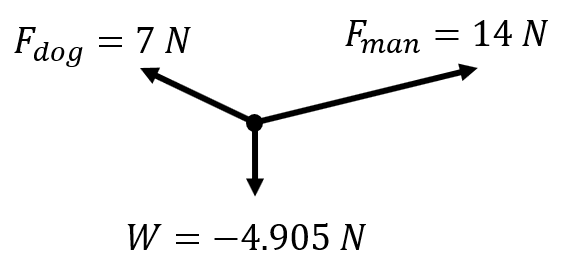
| A man and a dog are fighting over a chew toy. The man pulls up and to the right with a force of 14 N at 10° and the dog pulls up and to the left with 7 N of force at 15°. The dog toy accelerates horizontally only. What is the acceleration if the chew toy is 0.50 kg? |
|
\(\small\mathsf{ \overrightarrow{F}_{dog} = 7 \text{ N} }\), 165° \(\small\mathsf{ \overrightarrow{F}_{man} = 14 \text{ N} }\), 10° \(\small\mathsf{ \overrightarrow{F}_{gravity} = -4.905 \text{ N} }\) \(\small\mathsf{ \overrightarrow{F}_{net} = ? \text{ N} }\) \(\small\mathsf{ \overrightarrow{a} = ? \text{ m/s}^2 }\) \(\small\mathsf{ m = 0.50 \text{ kg} }\) |
\(\small\mathsf{ \overrightarrow{F}_{net} = \sum \overrightarrow{F} }\) \(\small\mathsf{ \overrightarrow{F} = m \overrightarrow{a} }\) |
Find the net force: \(\small\mathsf{ \overrightarrow{F}_{net} = 7(\cos{165°}) \text{ N} + 14(\cos{10°}) \text{ N} }\) \(\small\mathsf{ \overrightarrow{F}_{net} = -6.761 \text{ N} + 13.787 \text{ N} }\) \(\small\mathsf{ \overrightarrow{F}_{net} = 7.03 \text{ N} }\) Find the acceleration: \(\small\mathsf{ 7.03 \text{ N} = (0.50 \text{ kg}) \overrightarrow{a} }\) \(\small\mathsf{ \overrightarrow{a} = \frac{7.03 \text{ N}}{0.50 \text{ kg}} }\) \(\small\mathsf{ \overrightarrow{a} = 14.1 \text{ m/s}^2 }\) |