You can use your understanding of kinematics and work backwards to find a net force as well. Let's consider this example.
![Teen boy using a small boat]](https://s3.amazonaws.com/cms.accelerate-ed.com/image/5c829284-a78a-49fa-a29b-0ea9fd7c26c6.jpg)
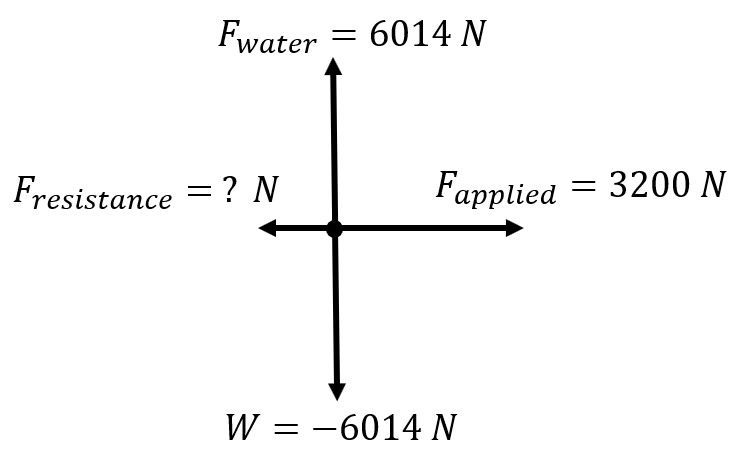
A 613 kg motorboat starts from rest in the water and accelerates to a speed of 25.4 m/s in 5.30 seconds. If the applied force on the boat is equal to 3200 Newtons, what is the force of resistance of the water on the boat?
You can break this problem down into three steps.
| Find the Acceleration | Use \(\mathsf{\overrightarrow{a} = \frac{\overrightarrow{v}_f - \overrightarrow{v}_i}{t} }\) to find the acceleration of the motor boat. |
| Find the Net Force | Use \(\small\mathsf{ \overrightarrow{F} = m \overrightarrow{a} }\) to find the net force on the motor boat. |
| Find the Force of Resistance | Use the sum of the forces to find the missing force: \(\small\mathsf{ \overrightarrow{F}_{x-net} = \sum \overrightarrow{F}_x }\) |
Work the problem out yourself and then check your work.
| Problem | Picture | Given/Find | Equation | Solution |
|---|---|---|---|---|
| A 613 kg motorboat starts from rest in the water and accelerates to a speed of 25.4 m/s in 5.30 seconds. If the applied force on the boat is equal to 3.20 x 103 Newtons, what is the force of resistance of the water on the boat? |
|
\(\small\mathsf{ \overrightarrow{F}_{applied} = 3200 \text{ N} }\) \(\small\mathsf{ \overrightarrow{F}_{resistance} = ? \text{ N} }\) \(\small\mathsf{ \overrightarrow{v}_i = 0 \text{ m/s} }\) \(\small\mathsf{ \overrightarrow{v}_f = 25.4 \text{ m/s} }\) \(\small\mathsf{ t = 5.30 \text{ s} }\) \(\small\mathsf{ m = 613 \text{ kg} }\) |
\(\mathsf{\overrightarrow{a} = \frac{\overrightarrow{v}_f - \overrightarrow{v}_i}{t} }\) \(\small\mathsf{ \overrightarrow{F} = m \overrightarrow{a} }\) \(\small\mathsf{ \overrightarrow{F}_{x-net} = \sum \overrightarrow{F}_x }\) |
Find the acceleration: \(\mathsf{\overrightarrow{a} = \frac{25.4 \text{ m/s} - 0}{5.30 \text{ s}} }\) \(\mathsf{\overrightarrow{a} = 4.79 \text{ m/s}^2 }\) Find the net force: \(\small\mathsf{ \overrightarrow{F} = (613 \text{ kg})(4.79 \text{ m/s}^2) }\) \(\small\mathsf{ \overrightarrow{F} = 2936.37 \text{ N} }\) Find the resistance force: \(\small\mathsf{ \overrightarrow{F}_{x-net} = \overrightarrow{F}_{applied} + \overrightarrow{F}_{resistance} }\) \(\small\mathsf{ 2936.37 \text{ N} = 3200 \text{ N} + \overrightarrow{F}_{resistance} }\) \(\small\mathsf{ -363.63 \text{ N} = \overrightarrow{F}_{resistance} }\) \(\small\mathsf{ \overrightarrow{F}_{resistance} = -264 \text{ N} }\) |