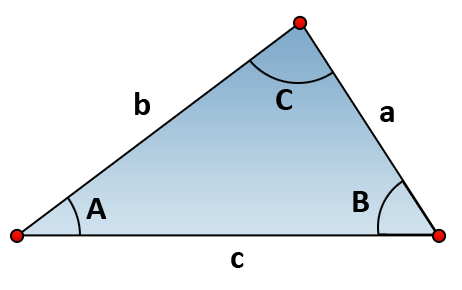
Take a closer look at the first triangle on this page, which you have seen before. Notice that capital letters are used to denote the angles (A, B, and C) and lower-case letters are used to denote the sides (a, b, and c). Also, each side marked with a lower-case letter appears across from its corresponding capital-letter angle.
The Law of Sines can be written in both of these ways:
\(\mathsf{ \frac{a}{sinA} }\) = \(\mathsf{ \frac{b}{sinB} }\) = \(\mathsf{ \frac{c}{sinC} }\)
or
\(\mathsf{ \frac{sinA}{a} }\) = \(\mathsf{ \frac{sinB}{b} }\) = \(\mathsf{ \frac{sinC}{c} }\)
How does it look when you use these ratios to describe actual triangles? Study each of the examples below.
Example 1
Example 2
Example 3
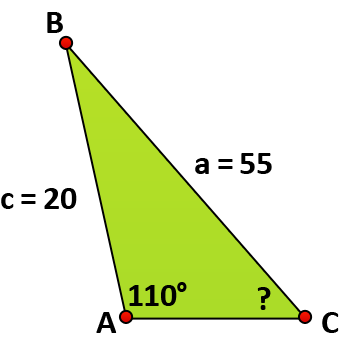
Suppose you are given the angle above and asked to find the measure of angle C. How could you use the Law of Sines to write a proportion that can help you solve for C? Think about the approach you would take. Then click the Show Me Button to compare your ideas to the tried and true method demonstrated below.

First identify what items you know:
\(\small\mathsf{ \angle }\)A = 110°
a = 55
c = 20
Next write the proportion using the Law of Sines:
\(\mathsf{ \frac{a}{sinA} }\) = \(\mathsf{ \frac{c}{sinC} }\)
\(\mathsf{ \frac{55}{sin110°} }\) = \(\mathsf{ \frac{20}{sinC} }\)
or
\(\mathsf{ \frac{sinA}{a} }\) = \(\mathsf{ \frac{sinC}{c} }\)
\(\mathsf{ \frac{sin110°}{55} }\) = \(\mathsf{ \frac{sinC}{20} }\)
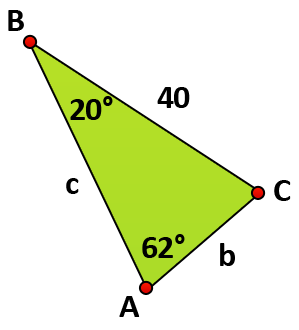
Let's look at another example. Suppose you are given the triangle above and asked to find side b. Use the Law of Sines to write a proportion, and then click on the Show Me Button below to check your work.

First identify the information you are given:
\(\small\mathsf{ \angle }\)A = 62°
a = 40
\(\small\mathsf{ \angle }\)B = 20°
Then use the Law of Sines to write a proportion:
\(\mathsf{ \frac{a}{sinA} }\) = \(\mathsf{ \frac{b}{sinB} }\)
\(\mathsf{ \frac{40}{sin62°} }\) = \(\mathsf{ \frac{b}{sin20°} }\)
or
\(\mathsf{ \frac{sinA}{a} }\) = \(\mathsf{ \frac{sinB}{b} }\)
\(\mathsf{ \frac{sin62°}{40} }\) = \(\mathsf{ \frac{sin20°}{b} }\)
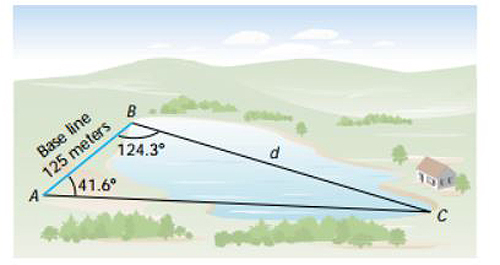
Let's look back at an earlier example. How might you tell the swim coach how far you swim when you train at home?

Identify the information you are given:
\(\small\mathsf{ {AB} }\) = 125
\(\small\mathsf{ \angle }\)A = 41.6°
\(\small\mathsf{ \angle }\)B = 124.3°
\(\small\mathsf{ \angle }\)C = 14.1°
Remember \(\small\mathsf{ \angle }\)A + \(\small\mathsf{ \angle }\)B + \(\small\mathsf{ \angle }\)C = 180°
\(\small\mathsf{ {BC} }\) = distance of swim = ?
Now use the Law of Sines to write a proportion:
\(\mathsf{ \frac{125}{sin14.1°} }\) = \(\mathsf{ \frac{BC}{sin41.6°} }\)
and solve the equation:
\(\small\mathsf{ {BC} }\) = 340.66 meters
The distance you cover when you swim at home should definitely impress the coach.
