So far we have been working with sine, cosine and tangent ratios, which apply only to right triangles. Fortunately or unfortunately, life is not made up entirely of right angles and triangles. What happens when you need to solve a problem that involves another kind of triangle? How do you find unknown distances/sides and angles in these shapes?
Consider triangle ABC, which does not include a right angle. Notice that sides a, b, and c are located opposite their corresponding angles--A, B, and C. These angles and sides are the components of a law that pertains to sine, the Law of Sines.
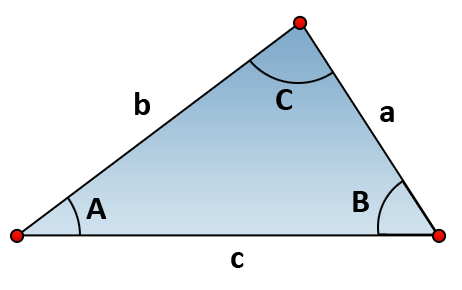
Law of Sines: \(\mathsf{ \frac{SinA}{a} }\) = \(\mathsf{ \frac{SinB}{b} }\) = \(\mathsf{ \frac{SinC}{c} }\)
We can use this law to calculate the length of the remaining sides of a triangle when two of the triangle's angles and one of its sides are known.
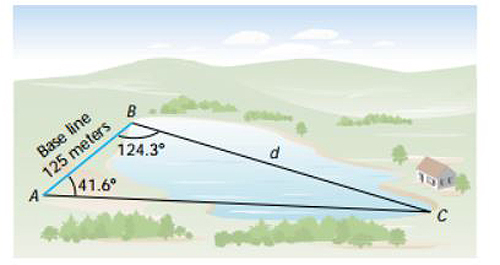
How does the Law of Sines apply outside your geometry classroom? Suppose you decide to try out for the swim team at your school. The coach asks, "How far can you swim?" You tell him that you often swim across the little lake in your back yard.
That answer doesn't give the coach much information, does it? You can use the Law of Sines, though, to figure out exactly how far you swim on a typical day, even though it would be impractical to measure the distance across the lake. This lesson will show you how.