Let's put everything together and work through a problem from start to finish. Remember that you must always check for the ambiguous case first. If the problem does not represent an ambiguous case, then you can keep working.
Here is the problem we'll tackle:
Solve a triangle with \(\small\mathsf{ \angle }\)A = 115°, \(\small\mathsf{ \angle }\)C = 35° and c = 200.
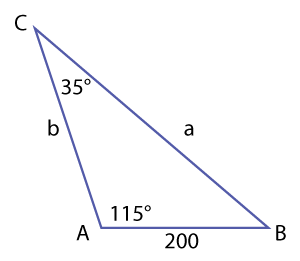
Step 1 - First draw the triangle--if it hasn't already been drawn for you as part of the problem. 
Step 2 - Next, figure out if the problem represents an ambiguous case. Since we are given two angles and a side, we do not have an ambiguous case. One triangle is created, and we can solve for the missing angle and sides. 
Step 3 - Write a proportion, using the Law of Sines, that helps you solve for the unknown side a. Then solve the equation.
\(\mathsf{ \frac{sinC}{c} }\) = \(\mathsf{ \frac{sinA}{a} }\)
Cross multiply: 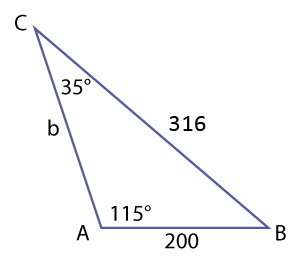
Step 4 - Now you need to find the measure of angle B. Remember that when you add the three angles of any triangle, the sum of the angle measures is always 180°. Write and solve an equation based on this property of triangles.
m\(\mathsf{ \angle }\)A + m\(\mathsf{ \angle }\)B + m\(\mathsf{ \angle }\)C = 180° 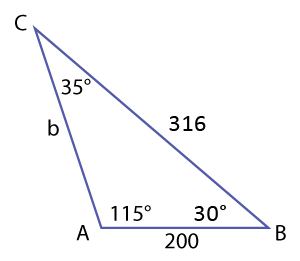
Step 5 - Now you need to solve for the last piece of the puzzle, side b. Write another proportion using the Law of Sines and solve for side b.
\(\mathsf{ \frac{sinC}{c} }\) = \(\mathsf{ \frac{sinB}{b} }\) |
