So far you have learned that you can use the Law of Sines on any triangle, and in particular triangles that are not right triangles. There are two cases, or types of problems, for which you should definitely use the Law of Sines. Each of these cases is described below
ASA
SAA
When the measure of two angles and the length of an included side are given as part of the problem, use the law of Sines to solve the problem. For example, you might know angles A and C and the included side b.
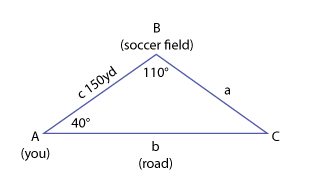
Let's take a look at how you might use the Law of Sines when you encounter this type of problem in your daily life. Suppose you're walking along a straight road and you see some friends playing soccer off to your left. They invite you to join them, so you leave the road and walk along a path that makes a 40° angle with the road. After 150 yards, you arrive at the soccer game. Later, after the game is over, you head back towards the road but this time along a different path that creates a 110° angle with the path you used earlier. How far will you need to walk on this new path to get back to the road?
To solve this problem, you'll need to first identify the information that is known or given, and then use the Law of Sines to set up a proportion that will give you a solution. Try solving the problem in your notebook. Then click the button below to check your work.

Identify the information you are given:
\(\small\mathsf{ \angle }\)A = 40°
\(\small\mathsf{ \angle }\)C = 30°, remember \(\small\mathsf{ \angle }\)A+\(\small\mathsf{ \angle }\)B+\(\small\mathsf{ \angle }\)C = 180°
c = 150 yards
Use the Law of Sines to write a proportion:
\(\mathsf{ \frac{sinC}{c} }\) = \(\mathsf{ \frac{sinA}{a} }\)
\(\mathsf{ \frac{sin30°}{150} }\) = \(\mathsf{ \frac{sin40°}{a} }\)
Solve for a:
a = 192.8 yards
When the length of a non-included side and the measures of two angles are given in the problem, you should again use the Law of Sines. For example, you might know the length of side c and the measure of angles A and C.

Now let's look at how you might use the Law of Sines with SAA using our previous example. Lets say that once you got back to the road (point C) you realized you dropped your wallet on the road before you headed off to play soccer. How far would you have to walk back along the road to find your wallet?
Work through this problem in your notebook. Then click the button below to check your work.

Identify the information you are given:
\(\small\mathsf{ \angle }\)A = 40°
a = 192.8 yards
\(\small\mathsf{ \angle }\)B = 110°
Use the Law of Sines to write a proportion and solve for b:
\(\mathsf{ \frac{sin40°}{192.8} }\) = \(\mathsf{ \frac{sin110°}{b} }\)
Solve for b:
b = 281.85 yards
