As you learned on the previous page, a problem represents an ambiguous case when it includes information about the length of two sides and the measure of one angle SSA. It's important to be able to recognize an ambiguous case immediately. If you don't identify a problem as ambiguous right away, you'll arrive at a partially correct answer, or you'll become frustrated trying to solve for a triangle that doesn't even exist.
The first step for identifying an ambiguous case is to find the height of the triangle. Can you remember the equation for the height? Click on the Show Me Button below to check your thinking.

h = bsinA
Let's review how the height and sides (a and b) compare in each case. Work through each tab to review the ambiguous case.
One Triangle
Two Triangles
No Triangles
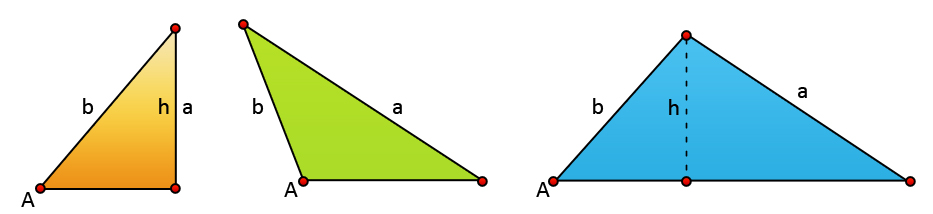
If angle A is acute and a = h, then one triangle is formed. Also, if angle A is acute or obtuse and a > b, one triangle is formed.
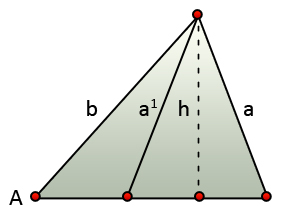
If angle A is acute and h < a < b, then two triangles are created.
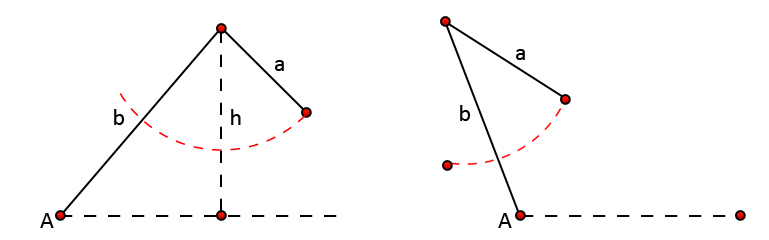
If angle A is acute and a < h, then no triangle is created. Also, if angle A is obtuse and a < b or a = b, then no triangle is created.
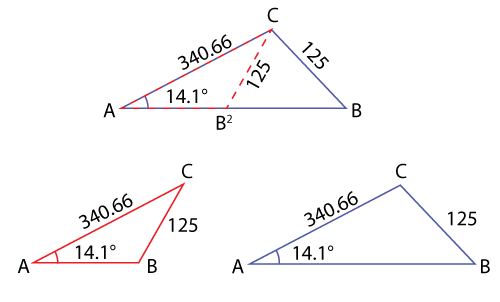
Suppose you are given the following triangle and asked to solve for all the missing sides and angles.
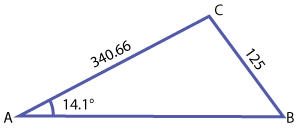
You should recognize that this is an ambiguous case of the Law of Sines since you are given one angle and two sides. Your first step is to decide if the information provided creates one triangle, two triangles, or no triangles. Let's work through the process together--before you click each step, try to guess what that step will involve.
| Step 1 | Identify whether angle A is acute or obtuse. | Since the measure of angle A is 14.1° the angle is acute. |
| Step 2 | Find h. | h = bsinA h = 340.66sin(14.1°) \(\mathsf{ \approx }\) 82.99 |
| Step 3 | Compare sides a, b and h. | Since h < a < b or in this case 82.99 < 125< 340.66, two triangles are created for this situation. |
Can you imagine how two triangles could have totally different shapes, but still have the three given criteria in common? In your notebook, draw how the two triangles might appear. Then click the button below to check your ideas.