You Try It

Now it's your turn to work through some problems. Remember that your first step is always to check for the ambiguous case. Solve the problem on each of the flashcards below before clicking the card to check your work.

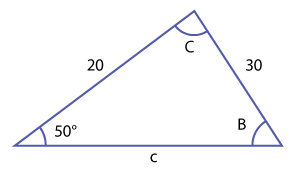
triangle with a 50° angle, 20 and 30 side.

A triangle has the following known angles and sides:

a = 30
b = 20
\(\small\mathsf{ \angle }\)A = 50°

Will this situation produce one triangle, two triangles, or no triangles?

Since this is a SSA triangle we do have an ambiguous case. The first step is to draw a picture.

Since \(\small\mathsf{ \angle }\)A is an acute angle and a > b, one triangle is formed.

Now that you know that only one triangle exists, find the measure of angle B.

Write the following proportion using the Law of Sines and then solve for the measure of angle B.

\(\mathsf{ \frac{sinA}{a} }\) = \(\mathsf{ \frac{sinB}{b} }\)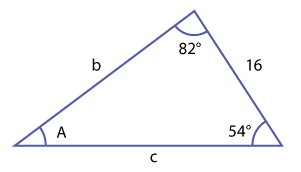

\(\mathsf{ \frac{sin50°}{30} }\) = \(\mathsf{ \frac{sinB}{20} }\)

sinB = \(\mathsf{ \frac{20(sin50°)}{30} }\)

sinB = 0.51

B = sin\(\mathsf{ ^{-1} }\)(0.52)

B \(\mathsf{ \approx }\) 30.7°

triangle with a 82° angle, 54° angle, and 16 side.

Solve for the missing side b, if possible. You know the following facts about triangle ABC.

\(\small\mathsf{ \angle }\)C = 82° \(\small\mathsf{ \angle }\)B = 54° a = 16

We know that this is not an ambiguous case because we have information about two angles and an included side--so next we draw the triangle.

In order to write a proportion using the Law of Sines we need to know angle A.

m\(\small\mathsf{ \angle }\)A + m\(\small\mathsf{ \angle }\)B + m\(\small\mathsf{ \angle }\)C = 180°

m\(\small\mathsf{ \angle }\)A + 54° + 82° = 180°

m\(\small\mathsf{ \angle }\)A = 44°

Now write a proportion and solve for b.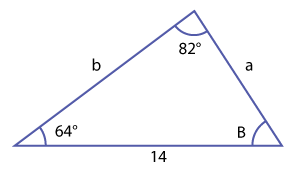

\(\mathsf{ \frac{sinA}{a} }\) = \(\mathsf{ \frac{sinB}{b} }\)

\(\mathsf{ \frac{sin44°}{16} }\) = \(\mathsf{ \frac{sin54°}{b} }\)

b(sin44°) = 16(sin54°)

b = \(\mathsf{ \frac{16(sin54°)}{sin44°} }\)

b \(\small\mathsf{ \approx }\) 18.6

triangle with a 82° angle, 64° angle, and 14 side.

Solve for the missing side a, if possible.

Write a proportion using the Law of Sines and then solve for the missing side a.

\(\mathsf{ \frac{sinA}{a} }\) = \(\mathsf{ \frac{sinC}{c} }\)

\(\mathsf{ \frac{sin64°}{a} }\) = \(\mathsf{ \frac{sin82°}{14} }\)

Cross multiply:

14(sin64°) = a(sin82°)

a = \(\mathsf{ \frac{14(sin64°)}{sin82°} }\)

a \(\small\mathsf{ \approx }\) 12.7

Text

Guided Notes

Tutor

Video

How To

Meet your new study partner! With our powerful Student Tools, your online learning experience just got more accessible, personalized, and thought-provoking than ever before!

Do you feel like you learn better when you watch videos? You’re not alone! Research shows instructional videos can make learners more engaged and active in online classes, when compared to text-only lessons.

Student Tools lets you turn some lesson pages into videos instantly! Just click the Student Tools tab and select Video. Remember, video instruction is not available on every lesson page.