You've seen a demonstration of how to use triangle properties to find the dimensions of a rectangle. You can use the sine, cosine, and tangent ratios to figure out the rectangle sides, and the Pythagorean theorem can help you calculate the rectangle's diagonal. You can even use the triangle's area to figure out the area of the rectangle containing it. Use the triangle properties you've learned to solve the problems in the tab set below.
Problem 1
Problem 2
Problem 3
Problem 4
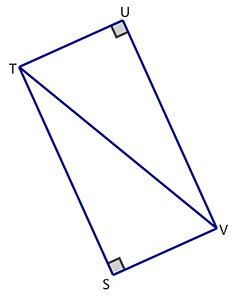
The area of △STV is 150 cm2. What is the area of rectangle STUV?
| Let's walk through the steps of solving this problem. How is the area of △STV related to the area of rectangle STUV? | The area of △STV is half the area of rectangle STUV. |
| Given this relationship, what is the area of rectangle STUV? | The area of rectangle STUV = 2*150 = 300 cm2. |
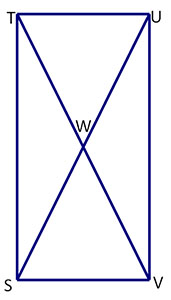
The cosine ratio of ∠TSU is \(\mathsf{ \small \frac{20}{25}}\). What is the length of segment SW?
| Since the cosine ratio of ∠TSU is \(\mathsf{ \small \frac{20}{25}}\), what is the length of diagonal SU? | \(\mathsf{\small{cosine = }\frac{adjacent}{hypotenuse}}\). Since SU is the hypotenuse, SU = 25. |
| Since diagonals SU and TV cross at point W, what do you know about segment SW? | The diagonals bisect each other at point W. Therefore, SW is half the length of SU. |
| Give the relations between SU and SW, what is the length of segment SW? | SW = \(\mathsf{ \small \frac{{SU}}{2} }\) = \(\mathsf{ \small \frac{25}{2} }\) = 12.5 |
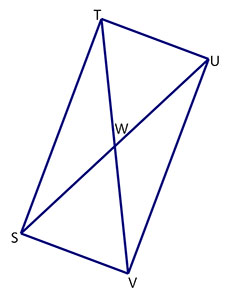
The tangent ratio of ∠SUV is \(\mathsf{ \small \frac{21}{28}}\). What is the length of segment TU?
| If the tangent ratio of ∠SUV is \(\mathsf{ \small \frac{21}{28}}\), what is the length of side SV? | \(\mathsf{\small{tangent = }\frac{opposite}{adjacent}}\). Since SV is the opposite side, SV = 21. |
| Because the figure is a rectangle, what is the relationship between SV and TU? | SV = TU |
| Therefore, what is the length of segment TU? | TU = 21 |
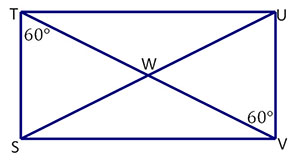
The length of segment WV is 8 cm. What is the area of rectangle STUV?
| What is the relationship between segments WV and TV? | The diagonals bisect each other at point W. Therefore, WV is half TV. |
| Given this relationship, what is the length of TV? | TV = 2*8 = 16 cm. |
| Since △STV is a 30-60 right triangle, what do you know about the side ratios? | The side ratios are 1:2:\(\mathsf{ \small \sqrt{3}}\) |
| Given these side ratios, what are the lengths of sides ST and SV? | ST = 8 and SV = 8\(\mathsf{ \small \sqrt{3}}\) |
| Now that you know the lengths of ST and SV, what is the area of rectangle STUV? | A = b*h = 8*8\(\mathsf{ \small \sqrt{3}}\) = 110.85 cm2 |
Did you understand how to work each of these problems? If not, go back and review what you don't understand. When you're ready to move forward, practice working a few problems more independently.
