The proofs on the previous page were fairly straight forward. The proof required to demonstrate this next statement is true is a bit more detailed, though.
Prove the diagonals of a rectangle bisect each other.
Read through the slide show below to see why this statement is true.
|
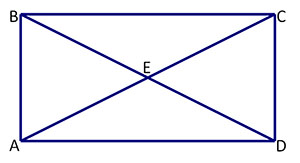
Consider rectangle ABCD.
The rectangle has 2 diagonals: AC and BD, and these diagonals cross at point E. We need to prove AE = EC and BE = ED.
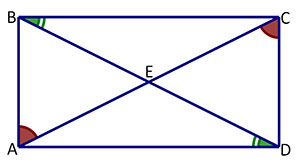
You know that △ABC ≅ △ADC by the side-angle-side (SAS) theorem. Therefore ∠BAC ≅ ∠DCA. Also, ∠ADB ≅ ∠CBD
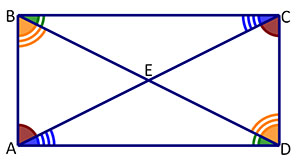
Next we can make use of the fact that rectangle ABCD is made of two right triangles. First, consider right angles ∟ABC and ∟CDA. Since both of these angles equal 90° and ∠ADB ≅ ∠CBD, you know that ∠ABD ≅ ∠CDB. Next, consider right angles ∟BAD and ∟DCB. Since both of these angles equal 90° and ∠BAC ≅ ∠DCA, you know that ∠CAD ≅ ∠ACB.
By the Angle-Side-Angle (ASA) theorem, you now have 2 sets of congruent triangles. △ABE ≅ △DCE and △BCE ≅ △ADE. By the definition of congruent triangles, AE ≅ EC and BE ≅ ED, thus AE = EC and BE = ED. Based on this proof, see if you can answer the question below.
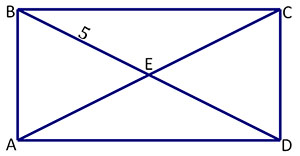
If BE = 5, what is the length of segment EC? The diagonals are congruent and bisect each other at point E. Therefore, EC = BE = 5. |