On the previous page, you saw how Olivia was able to use triangles to build rectangles. Now see if you understand what it takes to do the same, by answering each of the questions in the activity below.
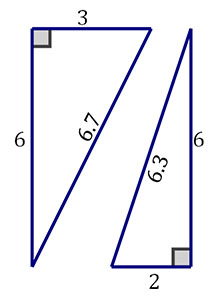
Can you use these two right triangles to build a rectangle?
- Yes
- No
- Maybe
A rectangle is composed of two congruent triangles and these triangles are NOT congruent.
A rectangle is composed of two congruent triangles and these triangles are NOT congruent.
A rectangle is composed of two congruent triangles and these triangles are NOT congruent.
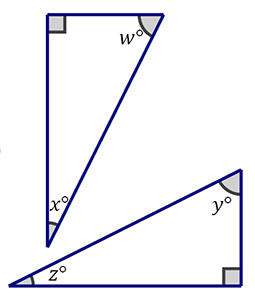
If you use these two congruent right triangles to build a rectangle, which two angles will combine to form a right angle?
- x° + w°
- x° + y°
- x° + z°
Angles x° and y° are complementary and therefore combine to form a right angle.
Angles x° and y° are complementary and therefore combine to form a right angle.
Angles x° and y° are complementary and therefore combine to form a right angle.
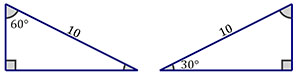
If you use these two congruent right triangles to build a rectangle, what will be the rectangle's area?
- 25\(\mathsf{\small\sqrt{3}}\)
- 5\(\mathsf{\small\sqrt{3}}\)
- 10\(\mathsf{\small\sqrt{3}}\)
A = bh = 5*5\(\mathsf{\small\sqrt{3}}\) = 25\(\mathsf{\small\sqrt{3}}\)
Use this formula to find the area: A = bh
Use this formula to find the area: A = bh
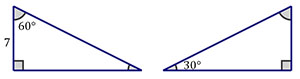
If you use these two congruent right triangles to build a rectangle, what will be the length of the rectangle's diagonal?
- 21
- 7
- 14
Remember, a rectangle's diagonal is really just one side of a right triangle, so you can use the Pythagorean formula to find its length.
Remember, a rectangle's diagonal is really just one side of a right triangle, so you can use the Pythagorean formula to find its length.
Remember, a rectangle's diagonal is really just one side of a right triangle, so you can use the Pythagorean formula to find its length.
Summary
Questions answered correctly:
Questions answered incorrectly:
