As you learned already in this lesson, the diagonal (D) of a rectangle can be calculated using the length (L) and width (W), in this way:
While properties like this are fairly easy to see, other properties of rectangles require a bit more examination, and you should expect to see any property proven formally before accepting it as true. Study the proofs on the tabs below to see how you can use right triangles to prove the less obvious properties of rectangles.
Proof 1
Proof 2
Prove the diagonal (D) of a rectangle can be calculated using the length (L) and width (W) of a rectangle, such that \(\mathsf{ \small{D = } \sqrt{L^2 + W^2} }\).
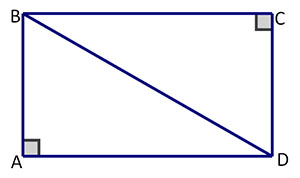
Consider rectangle ABCD. Let length (L) of the rectangle correspond to side AD in the triangle, width (W) correspond to triangle side AB, and diagonal d correspond to side BD, such that
L = AD
W = AB
D = BD
By the Pythagorean Theorem,
\(\mathsf{ \small{BD = } \sqrt{{AD}^2 + {AB}^2} }\)
By substitution,
\(\mathsf{ \small{D = } \sqrt{L^2 + W^2} }\)
Use this information to answer a question about the figure below.
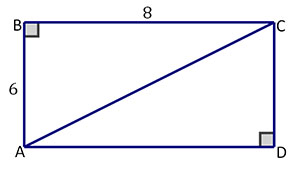
What is the length of diagonal AC?
\(\mathsf{ \small{{AC} = } \sqrt{6^2 + 8^2} { = 10}}\)
Prove the diagonals of a rectangle are congruent.

Rectangle ABCD has diagonals AC and BD. Consider △ABD and △ACD.
Since opposite sides of a rectangle are congruent, AB ≅ CD and BC ≅ AD.
Because rectangles have 4 right angles, you know that m∠DAB = m∠ADC = 90°.
Therefore, by SAS, △ABD ≅ △ACD.
Because the triangles are congruent, corresponding sides are congruent. Therefore, the hypotenuse of △ABD is congruent to the hypotenuse of △ACD. Hence, BD ≅ AC.
Therefore, the diagonals of a rectangle are congruent.
Use the information above to answer a question about the figure below.

If AC = 5, what is the length of BD?
AC = BD = 5
