How can you use right triangles to create rectangles? And once you build a rectangle this way, what can you assume to be true about the shape? As you will learn in this lesson, you can even use right triangles to determine the properties of a rectangle. The slides below will demonstrate how.
Tab 1
Tab 2
Tab 3
Tab 4
Tab 5
To understand how you can use triangles to build rectangles, you first need to think a little differently about what a rectangle is. Sure, you've been identifying rectangles since elementary school, but have you ever thought about the properties of a rectangle? What is the definition of rectangle, in the very precise language of geometry?
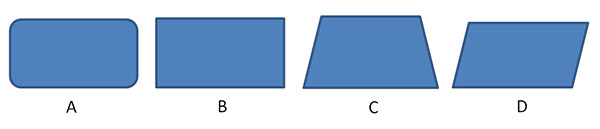
You probably can identify Figure B as a rectangle. But why are the other figures NOT rectangles? Why is Figure A, for instance, not a rectangle?
Figure A has curved edges while the edges of a rectangle form right angles.
Why is Figure C not a rectangle?
The shorter sides of Figure C are not parallel—the opposite sides of a rectangle are always parallel.
Why is Figure D not a rectangle?
Figure D has no right angles—every rectangle has 4 right angles.
On the previous tab, you identified several properties of rectangles:
- A rectangle has four straight sides.
- A rectangle has four right angles.
- A rectangle's opposite sides are parallel.
Because rectangles have four straight sides and 4 right angles, you can use right triangles to build rectangles--just as Olivia did in the beginning of this lesson. As an example, consider this rectangle.

What happens if you draw a diagonal across the rectangle connecting ∠A to ∠C?
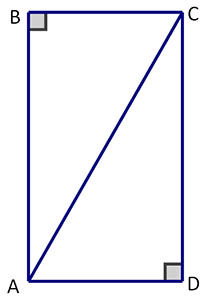
If you know that a diagonal is any line that connects opposite vertices of the rectangle, can you say how many diagonals a rectangle has, as a rule?
A rectangle has two diagonals—the vertices of ∠B and ∠D can also be connected by a diagonal. (This is another property of rectangles.)
Now recall what you've learned about right angles earlier in the course. What is the relationship between diagonals AC and BD?
AC ≅ BD (The diagonals in a rectangle are congruent.)

When you draw diagonal AC, what shapes are created inside the rectangle? Two triangles, right? But what type of triangles did you create by drawing a diagonal?
two right triangles
What is the best way to describe the relationship between these two right triangles?
The triangles are congruent. You know the triangles are congruent because of the Side-Angle-Side (SAS) Theorem. AB ≅ CD and BC ≅ AD. Also, ∠B = ∠D = 90°.
Since a rectangle contains two right triangles, you can use the triangle's properties to describe various aspects of the rectangle. For example, the figure below shows the lengths of the triangle's base and height.
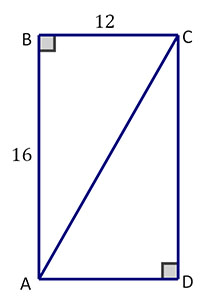
What is the length of diagonal AC?
You can use the Pythagorean Theorem to find AC: AC = \(\mathsf{\small\sqrt{{AB}^{2} + {BC}^{2}}}\) = \(\mathsf{\small\sqrt{16^{2} + 12^{2}}}\) = 20
Here's another example. The figure below shows the lengths of the triangle's hypotenuse and base.
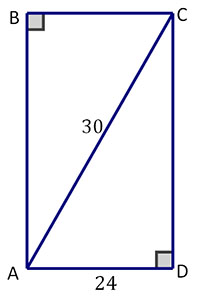
How can you use this information to calculate the perimeter of the rectangle (the distance around it)?
You can use the base and hypotenuse (and the Pythagorean formula) to discover the length of the missing sides of the rectangle.
CD = \(\mathsf{\small\sqrt{30^{2} - 24^{2}}}\) = 18
Then add the lengths of the sides:
Perimeter = 18 + 18 + 24 + 24 = 84
Suppose you build a rectangle using two special right triangles—such as this one containing two 30-60 right triangles.
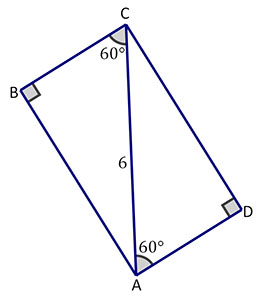
What is the leg ratio for a 30-60 right triangle?
1:2:\(\mathsf{\small\sqrt{3}}\)
Since the hypotenuse of the triangle is 6, what are the lengths of sides BC and AD?
BC = AD = 3
What are the lengths of sides AB and CD?
AB = CD = 3\(\mathsf{\small\sqrt{3}}\)
What is the area of the rectangle?
Area = (AB)(AD) = (3\(\mathsf{\small\sqrt{3}}\))(3) = 9\(\mathsf{\small\sqrt{3}}\)
What is the perimeter of the rectangle?
Perimeter = AB + BC + CD + AD = 2*3\(\mathsf{\small\sqrt{3}}\) + 2*3 = 6\(\mathsf{\small\sqrt{3}}\) + 6 ≈ 16.4
At this point, you should be able to answer the question posed at the beginning of this page: How can you combine right triangles to create rectangles?
Use two congruent triangles that are connected so that their hypotenuse forms the diagonal of the rectangle.
What do you know about a rectangle if you build it using special right triangles?
If you know one side of the special right triangle, you can use the leg ratios to calculate all four sides of the rectangle in addition to its area and perimeter.
How do you use right triangles to determine the properties of a specific rectangle?
You can use the Pythagorean Theorem to calculate the sides of the triangle, which will also tell you the sides of the rectangle. After you know the rectangle sides, you can calculate other properties of the rectangle. You can also use leg ratios if the rectangle contains special right triangles.
