You've practiced the steps involved in using right triangle properties to calculate the dimensions of a rectangle. Now solve a few problems on your own. Use the figure below to answer the questions that follow.
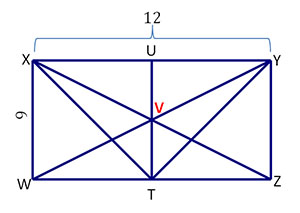
Which segments are diagonals of rectangle WXYZ?
- TY and XV and XZ
- XZ and WY and WV
- XZ and WY
- WV and VY
A diagonal connects opposite vertices of a rectangle, and a rectangle has two diagonals.
A diagonal connects opposite vertices of a rectangle, and a rectangle has two diagonals.
A diagonal connects opposite vertices of a rectangle, and a rectangle has two diagonals.
A diagonal connects opposite vertices of a rectangle, and a rectangle has two diagonals.
What is the length of XZ?
- 9\(\mathsf{ \small \sqrt{3}}\)
- 12
- 6\(\mathsf{ \small \sqrt{3}}\)
- 15
Since the diagonals of a rectangle are congruent, XZ = WY. By the Pythagorean Theorem, WY = \(\mathsf{ \small \sqrt{9^2+12^2}}\) = 15. Therefore, XZ = 15.
Since the diagonals of a rectangle are congruent, XZ = WY. By the Pythagorean Theorem, WY = \(\mathsf{ \small \sqrt{9^2+12^2}}\) = 15. Therefore, XZ = 15.
Since the diagonals of a rectangle are congruent, XZ = WY. By the Pythagorean Theorem, WY = \(\mathsf{ \small \sqrt{9^2+12^2}}\) = 15. Therefore, XZ = 15.
Since the diagonals of a rectangle are congruent, XZ = WY. By the Pythagorean Theorem, WY = \(\mathsf{ \small \sqrt{9^2+12^2}}\) = 15. Therefore, XZ = 15.
What is the length of WV?
- 7.5
- 15
- 5.7
- 21
The diagonals of this rectangle bisect each other at point V. Therefore, WV = \(\mathsf{ \small \frac{{WY}}{2}}\). Use the Pythagorean Theorem to get WY = 15. Hence WV = 7.5.
The diagonals of this rectangle bisect each other at point V. Therefore, WV = \(\mathsf{ \small \frac{{WY}}{2}}\). Use the Pythagorean Theorem to get WY = 15. Hence WV = 7.5.
The diagonals of this rectangle bisect each other at point V. Therefore, WV = \(\mathsf{ \small \frac{{WY}}{2}}\). Use the Pythagorean Theorem to get WY = 15. Hence WV = 7.5.
The diagonals of this rectangle bisect each other at point V. Therefore, WV = \(\mathsf{ \small \frac{{WY}}{2}}\). Use the Pythagorean Theorem to get WY = 15. Hence WV = 7.5.
What is the area of rectangle WXYZ?
- 54
- 108
- 216
- 62
A = b*h = 9*12 = 108
A = b*h = 9*12 = 108
A = b*h = 9*12 = 108
A = b*h = 9*12 = 108
What is the cosine ratio of ∠XYW?
- \(\mathsf{ \small \frac{12}{9} }\)
- \(\mathsf{ \small \frac{9}{12} }\)
- \(\mathsf{ \small \frac{15}{12} }\)
- \(\mathsf{ \small \frac{12}{15} }\)
\(\mathsf{ \small {cosine = }\frac{adjacent}{hypotenuse} \frac{12}{15} }\)
\(\mathsf{ \small {cosine = }\frac{adjacent}{hypotenuse} \frac{12}{15} }\)
\(\mathsf{ \small {cosine = }\frac{adjacent}{hypotenuse} \frac{12}{15} }\)
\(\mathsf{ \small {cosine = }\frac{adjacent}{hypotenuse} \frac{12}{15} }\)
Summary
Questions answered correctly:
Questions answered incorrectly:
