You can find the inverse of a relation or the inverse of a function. If you are given a set of (x, y) coordinate points, you simply need to reverse the domain (x) with the range (y) to create the inverse. If you need to find the inverse of a function, change the notation from \(f(x)\) to y, then interchange the x and the y in the equation and solve the equation for y. But once you find an inverse, how can you check to make sure it is actually the inverse you were looking for?
There are two ways to check inverses. You can graph the relation or function and its inverse, or, if the original relation was a function, then you can use composition of functions. Two functions are inverses when \( f\left( f^{- 1}\left( x \right) \right) = f^{- 1}\left( f\left( x \right) \right) = x \). For example:
Use a graph to show that the inverse of the relation
{(-3, -20); (-1, -12); (0, -8); (1, -4); (3, 4)} is {(-20, -3); (-12, -1); (-8, 0); (-4, 1); (4, 3)}.
When using a graph, the relation or function is an inverse if it is a reflection of the original relation or function over the line y = x. Since the graph shows that the points are reflections over the line y = x, these two relations are inverses of each other. |
Plot all the points, and then graph the line y = x. The points of the original relation are in black; the points of its inverse are in red, and the line y = x is in blue. 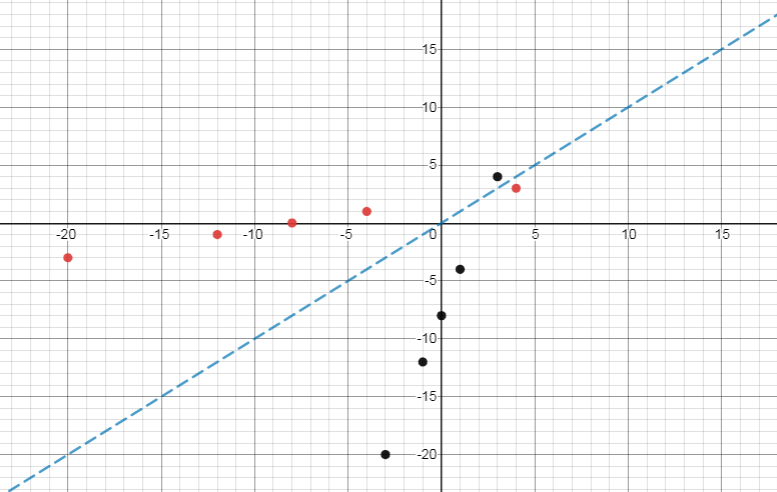
|
Use composition of functions to show that \( f\left( x \right) = 4x - 8 \) and \( f^{- 1}\left( x \right) = \frac{x + 8}{4} \) are inverses.
Find \( f\left( f^{- 1}\left( x \right) \right) \). |
\( f\left( f^{- 1}\left( x \right) \right) = f\left( \frac{x + 8}{4} \right) \) \( f\left( f^{- 1}\left( x \right) \right) = 4\left( \frac{x + 8}{4} \right) - 8 \) \( f\left( f^{- 1}\left( x \right) \right) = 4\left( \frac{x + 8}{4} \right) - 8 \) \( f\left( f^{- 1}\left( x \right) \right) = x + 8 - 8 \) \( f\left( f^{- 1}\left( x \right) \right) = x \) |
Find \( f^{- 1}\left( f\left( x \right) \right) \). |
\( f^{- 1}\left( f\left( x \right) \right) = f^{- 1}\left( 4x - 8 \right) \) \( f^{- 1}\left( f\left( x \right) \right) = \left( \frac{(4x - 8) + 8}{4} \right) \) \( f^{- 1}\left( f\left( x \right) \right) = \left( \frac{4x}{4} \right) \) \( f^{- 1}\left( f\left( x \right) \right) = x \) |
Since \( f\left( f^{- 1}\left( x \right) \right) = f^{- 1}\left( f\left( x \right) \right) = x \), the two functions are inverses of each other. |
|
How well can you use graphing and composition of functions to confirm that functions are inverses? Use the activity below to find out. Look at the pair of relations or pair of functions on each tab. Then use the requested method to show whether or not the two relations or functions are inverses of each other. Be sure to check your answers.
Use composition of functions to show that the inverse of \( f\left( x \right) = x^{3} + 3 \) is \( f^{- 1}\left( x \right) = \sqrt[3]{x - 3} \).
Show that \( f\left( f^{- 1}\left( x \right) \right) = f^{- 1}\left( f\left( x \right) \right) = x \). These two functions are inverses of each other. |
\( (f \cdot f^{-1})(x) = (f^{-1} \cdot f)(x) \) \( (\sqrt[3]{x - 3})^3 + 3 = \sqrt[3]{x^3+3 - 3} \) \( x - 3 + 3 = \sqrt[3]{x^3} \) \( x = x \) |
The graph of \( f\left( x \right) = x^{2} - 1 \) and of y = \( \pm \sqrt{x + 1} \) is shown below. Are these inverses? Explain.
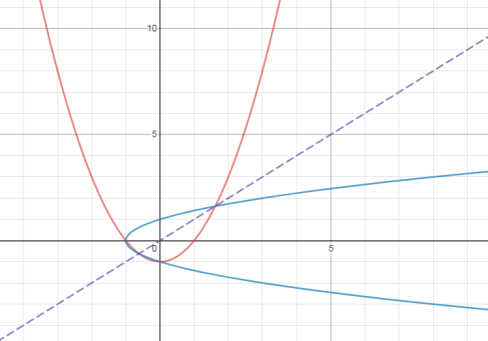
Yes, \( f\left( x \right) = x^{2} - 1 \) and \( y = \pm \sqrt{x + 1} \) are inverses of each other because their graphs are reflections of each other over the line y = x (shown in purple).
Use composition of functions to show that the inverse of \( f\left( x \right) = 3x - 4 \) is \( f^{- 1}\left( x \right) = \frac{x + 4}{3} \).
Show that \( f\left( f^{- 1}\left( x \right) \right) = f^{- 1}\left( f\left( x \right) \right) = x \). These two functions are inverses of each other. |
\( (f \cdot f^{-1})(x) = (f^{-1} \cdot f)(x) \) \( 3(\frac{(x+4)}{3}) - 4 = \frac{((3x - 4)+4)}{3} \) \( \cancel{3}(\frac{x+4)}{\cancel{3}} - 4 = \frac{3x}{3} \) \( x + 4- 4 = \frac{\cancel{3}x}{\cancel{3}} \) \( x = x \) |
