What is the difference between a relation and a function? Any set of inputs and outputs is considered a relation, but only a relation that has a unique output for each input is considered a function.
Reminder
A function is a relation that has a one-to-one relationship between the input values (domain) and the output values (range).
If you have the graph of a relation, you can use the vertical line test to determine whether the relation is a function. If the relation is a function, the vertical line will cross the graph only once—regardless of where the vertical line is drawn.
Complete the activity below to review and practice using the vertical line test to determine whether a relation is a function.
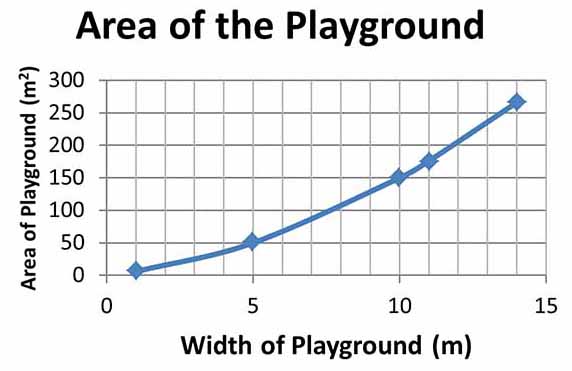
A rectangular playground is x meters wide and x + 5 meters long.
The formula for the area of the playground is A = (width)(length).
Substituting the quantities for the playground's width and length into the formula, \( A = x(x + 5) \).
Is this equation a function?
Use the table and graph below to answer.
| Width = \(x\) | A = \(x(x+5) \) | Area = \( (m^2) \) |
|---|---|---|
| 1 | 1(1 + 5) | 6 |
| 5 | 5(5 + 5) | 50 |
| 10 | 10(10 + 5) | 150 |
| 11 | 11(11 + 5) | 176 |
| 14 | 14(14 + 5) | 266 |
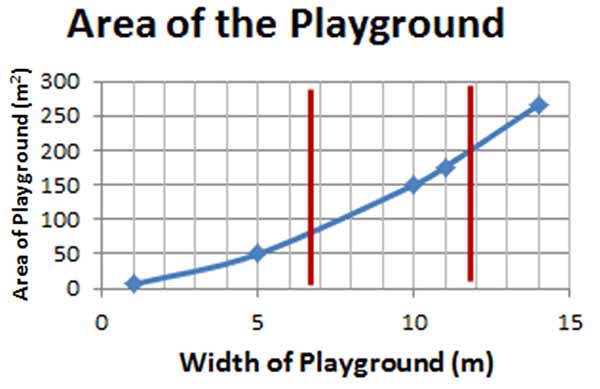
Use the vertical line test. Draw one or two vertical lines on the graph. Since the vertical lines pass through the curve only once, there is only one output for each input, and \( A = x(x + 5) \) represents a function. |
|
Registered nurses in a small town in Texas earn thirty dollars an hour. The equation y = 30x represents their gross pay.
Is this equation a function?
Use the table and graph below to answer.
| Hours Worded (hr) | 0 | 10 | 20 | 30 | 40 |
|---|---|---|---|---|---|
| Registered Nurse Salaary ($) |
0 | 300 | 600 | 900 | 1200 |
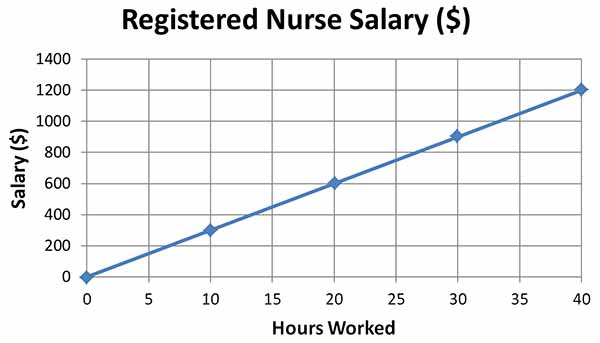
Use the vertical line test. Draw one or two vertical lines. Since the red vertical lines pass through the line only once, there is only one output for each input and \( y = 30x \) represents a function. |

|
The heights and ages of seven people were recorded in the table shown.
The equation for this graph is x = 160.
Is this equation a function?
Use the table and graph below to answer.
| Height (cm) | 160 | 160 | 160 | 160 | 160 | 160 | 160 |
|---|---|---|---|---|---|---|---|
| Age (years) | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
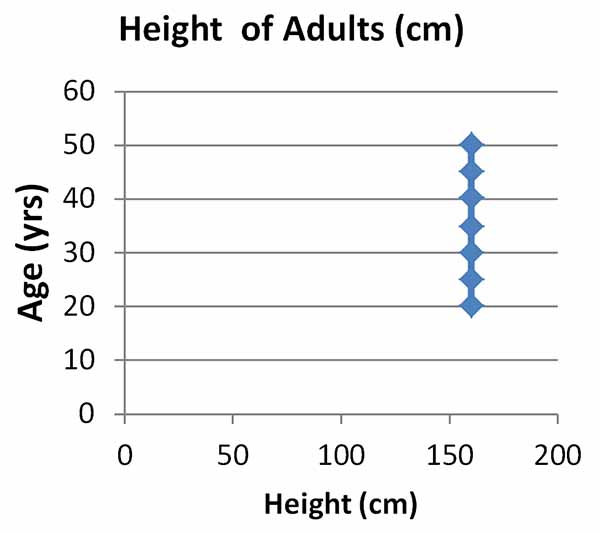
Use the vertical line test. Draw a line on the graph. Since this graph fails the vertical line test, there is more than one output for each input, and the equation x = 160 is not a function. |

|
Question
Is the relation \( y = \sqrt{x} \) a function? Explain.
Yes, the relation \( y = \sqrt{x} \) is a function. Finding the square root of a value only gives a positive result. Since each input is mapped to just one output, the relation is a function.
