Are you ready to take this lesson's quiz? The questions below will help you find out. Make sure you understand why each correct answer is correct--if you don't, review that part of the lesson.
Which is the inverse of {(1, -3), (2, -1), (3, 1), (4, 3), (5, 5)}?
- {(1, -3), (2, -1), (3, 1), (4, 3), (5, 5)}
- {(-3, 1), (-1, 2), (1, 3), (3, 4), (5, 5)}
- {(-3, -3), (-1, -1), (1, 1), (3, 3), (5, 5)}
- {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5)}
Interchange the domain and range of the original relation to find the inverse relation.
Interchange the domain and range of the original relation to find the inverse relation.
Interchange the domain and range of the original relation to find the inverse relation.
Interchange the domain and range of the original relation to find the inverse relation.
Which is a step in algebraically finding the inverse of a function?
- Graph the equation and then flip the graph.
- Solve the equation for x.
- Substitute real numbers and get a table of values.
- Interchange the x for the y and then solve for y.
To find the inverse of a function, change the notation from f(x) to y, interchange the x and the y in the equation, and then solve for y.
To find the inverse of a function, change the notation from f(x) to y, interchange the x and the y in the equation, and then solve for y.
To find the inverse of a function, change the notation from f(x) to y, interchange the x and the y in the equation, and then solve for y.
To find the inverse of a function, change the notation from f(x) to y, interchange the x and the y in the equation, and then solve for y.
What is the inverse of the function \( f(x) = \frac{x + 5}{4} \)?
- \( f^{-1}(x) = 4x + 5 \)
- \( f^{-1}(x) = 4x - 5 \)
- \( f^{-1}(x) = \frac{x - 5}{4} \)
- \( f^{-1}(x) = \frac{x + 5}{4} \)
To find the inverse of a function, change the notation from f(x) to y, interchange the x and the y in the equation, and then solve for y.
To find the inverse of a function, change the notation from f(x) to y, interchange the x and the y in the equation, and then solve for y.
To find the inverse of a function, change the notation from f(x) to y, interchange the x and the y in the equation, and then solve for y.
To find the inverse of a function, change the notation from f(x) to y, interchange the x and the y in the equation, and then solve for y.
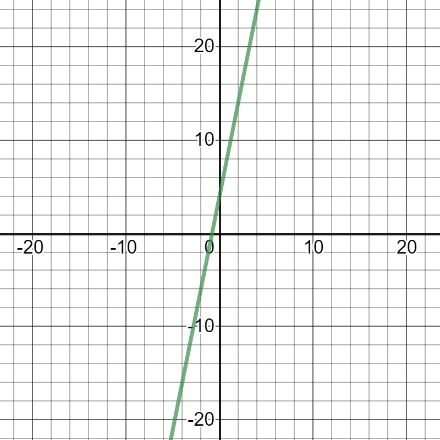
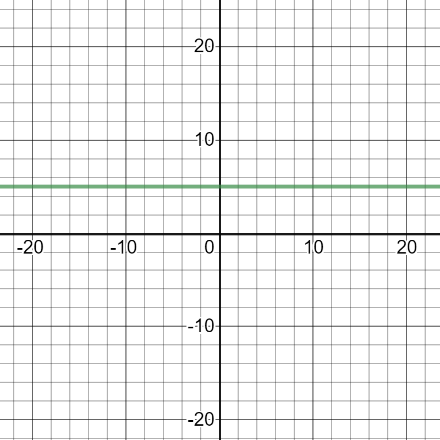
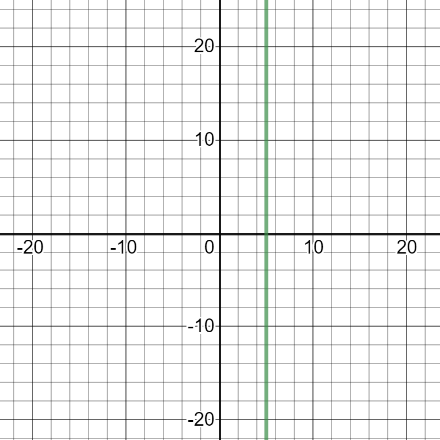
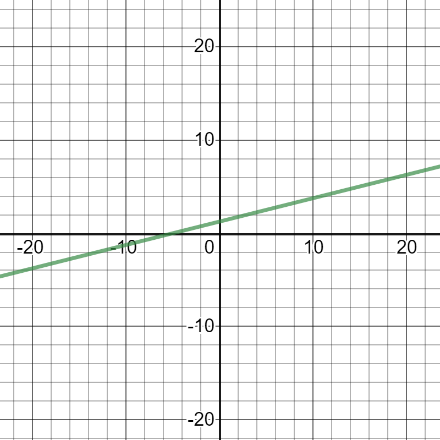
Which of the following is an inverse of the function shown in the graph below?
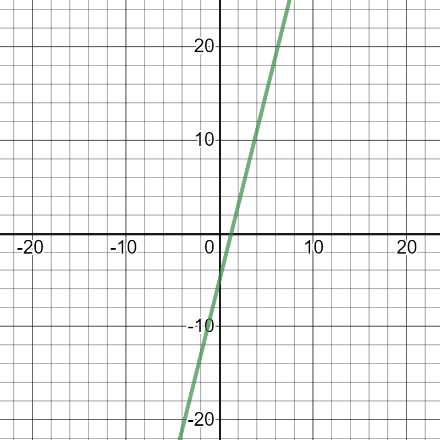

Find the graph that is a reflection of the given line over the line \( y = x \).
Find the graph that is a reflection of the given line over the line \( y = x \).
Find the graph that is a reflection of the given line over the line \( y = x \).
Find the graph that is a reflection of the given line over the line \( y = x \).
Which of the following is true about inverse functions?
- Their graphs are reflections of each other over the line \( y = x^{2} \).
- Their graphs exist solely in the first quadrant.
- The compositions are \( f\left( f^{- 1}\left( x \right) \right) = f^{- 1}\left( f\left( x \right) \right) = x \).
- The compositions are \( f\left( f^{- 1}\left( x \right) \right) = f^{- 1}\left( f\left( x \right) \right) = x^{2} \).
The graphs of inverse functions are reflections of each other over the line y = x.
The graphs of the functions may exist in any quadrant.
When functions are inverses of each other, both of their compositions are equal to x.
When functions are inverses of each other, both of their compositions are equal to x.
Summary
Questions answered correctly:
Questions answered incorrectly: