When two relations or functions are inverses of each other, the domain of the first is the range of the second, and the range of the first is the domain of the second. The notation for an inverse is \( f^{- 1}(x) \). But how do you find the inverse of a function?
In the video below, the instructor will review the definition of a function; then, he will show you how to use algebraic techniques to find the inverse of a function. In the video, the instructor will mention the term implicit form. This term means that the dependent variable (usually y) is not explicitly expressed in terms of the independent variable (usually x). The equation \( x^{2} + y^{2} = 1 \) is an implicit equation.
As you watch the video, pay close attention to how to use the composition of functions to check whether a pair of functions are inverses of each other.
You may want to download the study guide to follow along. If so, click the link below.
Hello, in this video, I’d like to share some information about function inverses. Function inverses essentially allow us to work backwards through a function in order to help solve for unknown variables. Let me explain. A function, is a mathematical device that takes an input value, applies a series of mathematical operations and maps it to a unique output value. For example, a collection of input values… would map to a collection of output values… with this function, f(x)=1/2 x2-3. We use the function to determine where each input maps to, and you might notice that some outputs were mapped by different inputs, which is okay. But no input maps to more than one input – this is required of all functions. If a mathematical operation maps an input to more than one output, it would be considered a relation, not a function.
The question for now, is how would we work backwards through a function? What if I know a function’s output, and I’d like to find the input that mapped to it? Generally, we use the inverse of a function to work backwards. Although there are methods that use graphs to do the same.
Let’s start with our function from above and find its inverse. A common method for finding an inverse is to first rewrite our function using “y equals” notation rather than function notation. This makes our work a little bit easier to follow on paper. Then we switch the x and y values… We do this since we are looking for the opposite of the original function. Since x is sometimes considered the opposite of y, this switch allows us to proceed towards the inverse, by solving for the new y value. To solve for y in this case, we must isolate it by first adding three to both sides of the equation… Then multiply by two on both sides of the equation to eliminate the one-half… Technically, this equation is the inverse of the original, although it is written in an implicit form. In other words, neither x nor y are completely isolated. However, if we take the square root of each side to solve for y… you’ll notice this is not a true function since you must include both a positive and negative result of the root to satisfy the domain and range of the original equation. When the inverse is finally determined, and you are certain that the inverse is also a function, you should record it using function inverse notation, which includes a negative one written between the f and x. However, in this example, the inverse is not a function and therefore should be written using standard y equals notation. Again, since the remaining operation maps some inputs to more than one output, this inverse is not considered a function. It is a relation.
If we try another, f(x)=x3-7, we would rewrite using “y equals” notation… Switch the x and y… Then add seven to both sides of the equation… And finally apply a cube root to both sides of the equation and write using function inverse notation...[f(-1) (x)=∛(x+7)] Since a cube root doesn’t have the same domain restrictions as a square root, we don’t use a positive and negative form of the root.
To check your work, we can verify if two functions are inverses if they compose with one another back to the identity, or x. Let’s check with our most recent example. The function f composed with f-inverse would require something cubed minus seven to act as our outer function… and the cube root of the quantity x plus seven will act as the interior function… If we simplify the function… we see a result of x. Now check the composition in the other direction… and it too simplifies to x. It is important to check the composition in both directions to verify the inverses.
To finish the video, I’ll provide two sample functions and show how to derive their inverses. I would like you to graph each pair of functions and inverses from this video to see if you can understand how the graph of functions and inverses can be used to check your work. Good luck!
Is the inverse of a function also a function?
- No, the inverse of a function is never a function.
- Yes, the inverse of a function is always a function.
- Maybe; the inverse of a function is sometimes a function.
Depending on the original function, its inverse may or may not be a function.
Depending on the original function, its inverse may or may not be a function.
Depending on the original function, its inverse may or may not be a function.
How can you use algebraic means to verify if two functions are inverses of each other?
- Create the composition \( f(f^{- 1}\left( x \right)) \). If this composition is equal to y, then the functions are compositions of each other.
- Create the compositions \( f(f^{- 1}\left( x \right)) \) and \( f^{- 1}(f\left( x \right)) \). If these are both equal to x, then the functions are compositions of each other.
- Create the composition \( f^{- 1}(f\left( x \right)) \). If this composition is a function, then the functions are compositions of each other.
Two functions are inverses of each other when the compositions \( f\left( f^{- 1}\left( x \right) \right) = f^{- 1}\left( f\left( x \right) \right) = x \).
Two functions are inverses of each other when the compositions \( f\left( f^{- 1}\left( x \right) \right) = f^{- 1}\left( f\left( x \right) \right) = x \).
Two functions are inverses of each other when the compositions \( f\left( f^{- 1}\left( x \right) \right) = f^{- 1}\left( f\left( x \right) \right) = x \).
The graph shows the inverse functions \( f\left( x \right) = 4x - 8 \) and \( f^{- 1}\left( x \right) = \frac{x + 8}{4}. \) It also shows the linear equation \( y = x \). How can you tell that these two functions are inverses of each other by looking at the graph?
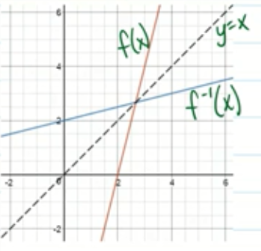

- Since the two functions have positive slopes as does the line y = x, they are inverses of each other.
- Since the two functions are reflections of each other over the line y = x, they are inverses.
- Since the two functions and the line y = x intersect in the first quadrant, they are inverses of each other.
When two functions are inverses, they will graph as reflections of each other over the line \( y = x \).
When two functions are inverses, they will graph as reflections of each other over the line \( y = x \).
When two functions are inverses, they will graph as reflections of each other over the line \( y = x \).
Summary
Questions answered correctly:
Questions answered incorrectly:
