Another characteristic of a population is population density, which is calculated by dividing the population size by the area of land that population inhabits. Population density is an important characteristic because it tells us how many individuals there are per unit of land--in other words, how crowded the population is.
$$\large\mathsf{\text{Population Density} = \frac{\text{Population Size}}{\text{Inhabited Area}}}$$
However, recall that it can be difficult to count every member of a population. Watch the video below to see an example of how challenging it can be to directly measure population size.
As of 2014, it was estimated that there are over 318 million residents of the United States. Imagine trying to count every human in the United States at a single moment!
All over the country, babies are being born and people are dying. The population is constantly increasing and decreasing in size.
If we know the size of our population, we can be better prepared to feed everyone, give everyone access to healthcare, and educate our nation’s children.
If we don’t know how many people we have, it is harder to manage our resources and plan for the future. But counting 318 million people is no easy task. There has to be a better way, but what could it be?
Instead of counting everyone and dividing by the entire inhabited area, we can pick a small section and just count the individuals within it. If we divide the number of individuals by the sampled area, we get population density. For example, let’s say we’ve sampled a rectangular section of a field and counted the number of cotton mice in the section. If the rectangular section is 4 km long and 2 km wide, the area of the sampled section is 4 km x 2 km = 8 km2. If there were 64 mice, the population density would be 64 mice / 8 km2, or 8 mice / km2.
Population density can also help us estimate the size of the entire population if it is too hard to count every individual. If we know the entire area of land, we can multiply that area by the density to get an estimate of the total population. If the field from the mouse population we’ve sampled is actually 100 km2, we can estimate the size of the entire population:
100 km2 x 8 mice/km2 = 800 mice
Many populations are too large or too mobile to count, so it is common to sample a small section and calculate population density and then use the land area to estimate population size.
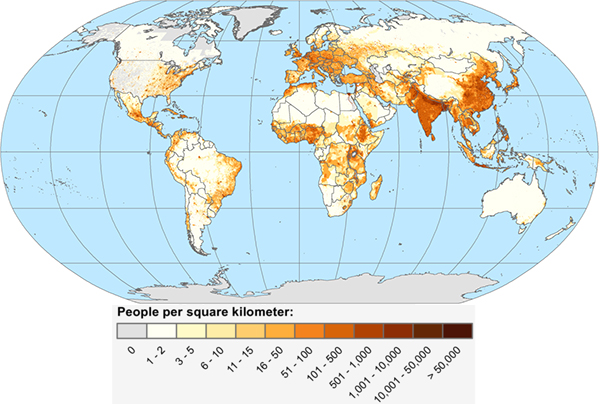
However, this process of estimating population size has its limitations. Populations are often not distributed evenly across their habitat area. For example, humans are not distributed evenly across the world as you can see in this image. Instead, humans are highly concentrated in a few areas (e.g., central Europe, India, China), less concentrated in many others (e.g., midwestern United States, southern Russia), and almost completely absent in others (e.g., Antarctica, most of Australia). If we calculate the population density of people in each country, we will get many different numbers. Thus, the accuracy of using population density to estimate population size depends on a well-chosen sampling area.
Population density of humans per square kilometer (km2) in 2010
Question
Imagine you are trying to estimate the number of humans on Earth. Your sample area is the country of India. Would you overestimate or underestimate the number of humans on Earth?
