In 1984, a television cartoon called The Transformers was introduced. It quickly became a favorite of children everywhere, and a series of toys were released. The toys mimicked the characters in the cartoons: robotic aliens that could transform themselves into cars, trucks, semis, or electronic items. Due to their immense popularity, The Transformers were soon on clothing and food products, and they also starred in a movie series. You may even have seen the 2017 movie, Transformers: The Last Knight.


Bumblebee is a robotic alien who can transform into a yellow automobile.
One of the more popular characters in the series is Bumblebee. He can transform from his alien robot form into a sports car. You can think of his alien robot shape as his natural or "parent" state of being. The sports car is his transformation. This is similar to how you can change the graphs of quadratic functions from the parent form into something else.

\( f\left( x \right) = x^{2} \)
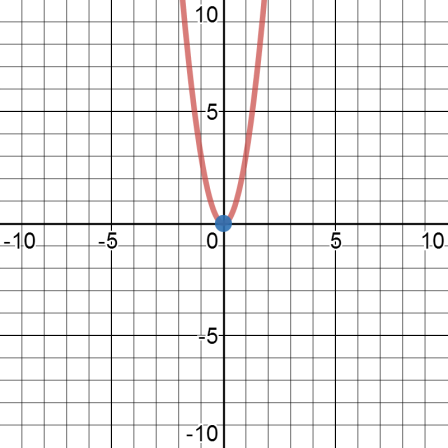
\( g\left( x \right) = 3x^{2} \)
Notice that both graphs are parabolas, both of them open up, and they both have the same vertex, (0, 0). But the graph of g(x) is vertically stretched compared to the graph of f(x).
Vertical stretching means the graph of the function is stretched out vertically, so its taller. A function that is vertically stretched has bigger y-values for any given value of x.
The graph of g(x) is a transformation of the graph of f(x).
In this lesson, you will learn how to rewrite the standard form of a quadratic function into a form that is easier to graph. You will then use the new form of the function to transform the graph of the parent quadratic function.
