Are you ready to take this lesson's quiz? The questions below will help you find out. Make sure you understand why each correct answer is correct--if you don't, review that part of the lesson.
Find the vertex of \( f\left( x \right) = - 3x^{2} + 6x + 5 \).
- \( ( - 3, - 24) \)
- \( ( - 1,\ 8) \)
- \( ( - 3,\ 8) \)
- \( (1,\ 8) \)
Complete the square to write the function in vertex form. The vertex form of a quadratic function is \( f\left( x \right) = a{(x - h)}^{2} + k. \) The vertex is located at \( \left( h,\ k \right) \).
Complete the square to write the function in vertex form. The vertex form of a quadratic function is \( f\left( x \right) = a{(x - h)}^{2} + k. \) The vertex is located at \( \left( h,\ k \right) \).
Complete the square to write the function in vertex form. The vertex form of a quadratic function is \( f\left( x \right) = a{(x - h)}^{2} + k. \) The vertex is located at \( \left( h,\ k \right) \).
Complete the square to write the function in vertex form. The vertex form of a quadratic function is \( f\left( x \right) = a{(x - h)}^{2} + k. \) The vertex is located at \( \left( h,\ k \right) \).
Which is the parent quadratic function?
- \( g\left( x \right) = x^{2} \)
- \( g\left( x \right) = \left( x + 1 \right) - 5 \)
- \( g\left( x \right) = x^{4} \)
- \( g\left( x \right) = {- \left( x + 2 \right)}^{3} - 7 \)
The parent quadratic function opens up, and its largest exponent is 2.
The parent quadratic function opens up, and its largest exponent is 2.
The parent quadratic function opens up, and its largest exponent is 2.
The parent quadratic function opens up, and its largest exponent is 2.
Explain the best way to graph the function \( h\left( x \right) = {2x}^{2} - 4x - 6 \).
- Choose values for \( h(x) \), substitute those values into the function, and solve for the output. Plot the resulting ordered pairs and connect them using a smooth curve.
- Write the function in standard form, and read the vertex from the function. Plot the vertex and then use the symmetrical nature of the parabola to plot the rest of the curve.
- Choose values for x, substitute those values into the function, and solve for the output. Plot the resulting ordered pairs and connect them using a smooth curve.
- Compare the given function to the parent quadratic function and determine what changes need to occur in order to plot \( h(x) \).
To graph a function in standard form, you should start by choosing values for the input variable.
This function is already written in standard form.
When graphing a function in standard form, you should start by choosing values for the input variable.
You cannot compare the given function to the parent function without rewriting \( h(x) \) in vertex form.
State the vertex form of \( g\left( x \right) = {3x}^{2} + 6x - 9 \).
- \( g\left( x \right) = - 3({x + 1)}^{2} - 6 \)
- \( g\left( x \right) = 3({x + 1)}^{2} - 12 \)
- \( g\left( x \right) = - 3({x - 1)}^{2} - 12 \)
- \( g\left( x \right) = 3({x + 1)}^{2} + 6 \)
Complete the square to find the vertex form of the function. Pay close attention to the signs.
Complete the square to find the vertex form of the function.
Complete the square to find the vertex form of the function. Pay close attention to the signs.
Complete the square to find the vertex form of the function. Pay close attention to the signs.
Describe how the value of a affects the graph of \( f\left( x \right) = {- 5x}^{2} + 10x - 13 \) when compared to the graph of the parent quadratic function.
- The value of \( a = - 5 \). Since \( a < 0, \) the parabola will open down. It will be stretched taller than the parent function by a factor of 5.
- The value of \( a = - 5 \). Since \( a < 0, \) the parabola will open up. It will be stretched taller than the parent function by a factor of 5.
- The value of \( a = - 5 \). Since \( a < 0, \) the parabola will open down. It will be compressed shorter than the parent function by a factor of 5.
- The value of \( a = - 5 \). Since \( a < 0, \) the parabola will open up. It will be compressed shorter than the parent function by a factor of 5.
The parabola will open upward if \( a > 0 \), and downward if \( a < 0 \). When compared to the parent quadratic function, the parabola is stretched taller if \( \left| a \right| > 1 \)and compressed shorter if \( 0 < \left| a \right| < 1 \).
The parabola will open upward if \( a > 0 \), and downward if \( a < 0 \). When compared to the parent quadratic function, the parabola is stretched taller if \( \left| a \right| > 1 \) and compressed shorter if \( 0 < \left| a \right| < 1 \).
The parabola will open upward if \( a > 0 \), and downward if \( a < 0 \). When compared to the parent quadratic function, the parabola is stretched taller if \( \left| a \right| > 1 \) and compressed shorter if \( 0 < \left| a \right| < 1 \).
The parabola will open upward if \( a > 0 \), and downward if \( a < 0 \). When compared to the parent quadratic function, the parabola is stretched taller if \( \left| a \right| > 1 \) and compressed shorter if \( 0 < \left| a \right| < 1 \).
Which is the equivalent standard form of \( f\left( x \right) = 3\left( x + 2 \right)^{2} - 5 \)?
- \( f\left( x \right) = 3x^{2} + 6x - 5 \)
- \( f\left( x \right) = 3x^{2} + 6x + 1 \)
- \( f\left( x \right) = 3x^{2} + 12x + 17 \)
- \( f\left( x \right) = 3x^{2} + 12x + 7 \)
Expand the square binomial. Multiply the resulting trinomial by the value of a. Then combine like terms.
Expand the square binomial. Multiply the resulting trinomial by the value of a. Then combine like terms.
Expand the square binomial. Multiply the resulting trinomial by the value of a. Then combine like terms.
Expand the square binomial. Multiply the resulting trinomial by the value of a. Then combine like terms.
Which is a step you must complete when writing \( f\left( x \right) = {2x}^{2} + 8x + 7 \) in vertex form?
- Choose values for the input variable, substitute those values into the function, and solve for the output.
- Divide the b term by 2 and then square the result.
- Multiply so that the value of \( a \neq 1 \).
- Connect the points with a smooth curve.
This is a step to complete when graphing a quadratic function in standard form.
You must complete this step to determine the value to add inside and outside the parentheses.
This is not a step to complete when writing a quadratic function in vertex form.
This is step to complete when graphing a quadratic function.
How does the graph of the quadratic function \( h\left( x \right) = 3{(x - 2)}^{2} + 5 \) compare to the graph of its parent function \( f\left( x \right) = x^{2} \)?
- When compared to the parent quadratic function, \( h(x) \) has a vertex at (3, 5). Both \( f(x) \) and \( h(x) \) open up and both are the same height.
- When compared to the parent quadratic function, \( h(x) \) has a vertex at (\( - \)2, 5). Both \( f(x) \) and \( h(x) \) open up, but \( h(x) \) is compressed shorter than \( f(x). \)
- When compared to the parent quadratic function, \( h(x) \) has a vertex at (\( - \)6, 5). Both \( f(x) \) and \( h(x) \) open up, but \( h(x) \) is stretched taller than \( f(x). \)
- When compared to the parent quadratic function, \( h(x) \) has a vertex at (2, 5). Both \( f(x) \) and \( h(x) \) open up, but \( h(x) \) is vertically stretched compared to \( f(x). \)
Identify the vertex and a-value and compare \( h(x) \) to the parent quadratic function, \( f\left( x \right) = x^{2} \).
Rewrite \( h\left( x \right) \) in vertex form by completing the square. Then compare \( h(x) \) to the parent quadratic function, \( f\left( x \right) = x^{2} \).
Rewrite \( h\left( x \right) \) in vertex form by completing the square. Then compare \( h(x) \) to the parent quadratic function, \( f\left( x \right) = x^{2} \).
Rewrite \( h\left( x \right) \) in vertex form by completing the square. Then compare \( h(x) \) to the parent quadratic function, \( f\left( x \right) = x^{2} \).
In the graph below, the green curve is the parent quadratic function, and the red curve is a transformation of the parent quadratic function. Compare the two functions.
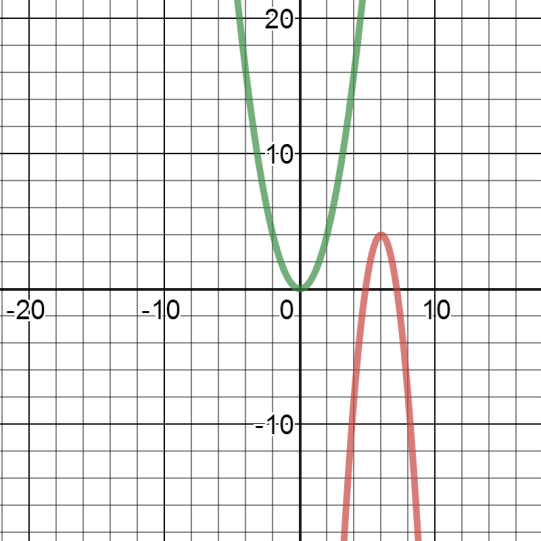

- Compared to the parent quadratic function, the red curve has a vertex at (6, 4). It opens down while the parent function opens up. The red curve is stretched taller than the green curve.
- Compared to the parent quadratic function, the red curve has a vertex at (0, 0). The red curve opens down while the parent function opens up. The red curve is compressed shorter than the green curve.
- Compared to the parent quadratic function, the red curve has a vertex at (3, 2). The red curve opens down while the parent function opens up. The red curve is compressed shorter than the green curve.
- Compared to the parent quadratic function, the red curve has a vertex at (8, 0). The red curve opens down while the parent function opens up. The red curve is stretched taller than the green curve.
Use the given graph to compare the parent quadratic function to this transformation.
Use the given graph to compare the parent quadratic function to this transformation.
Use the given graph to compare the parent quadratic function to this transformation.
Use the given graph to compare the parent quadratic function to this transformation.
Summary
Questions answered correctly:
Questions answered incorrectly:
