When a quadratic function is written in vertex form, you can use the values of a, h, and k to create the graph of the quadratic function. That graph is a transformation of the graph of the parent quadratic function, \( f\left( x \right) = x^{2} \).
It's your turn to practice graphing quadratic functions. Remember to rewrite the quadratic function in vertex form if needed. Then identify the vertex, determine how the value of \( a \) will affect the graph, and use the key points from the parent function to help you create the transformed graph.
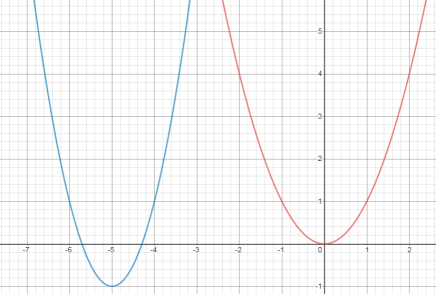
Graph \( f\left( x \right) = 2\left( x + 5 \right)^{2} - 1 \) using transformations.
The graph is shown. The blue curve is \( f\left( x \right) = 2\left( x + 5 \right)^{2} - 1 \). The red curve is the parent function. It is shown for reference.
If you need help arriving at this answer, click the solution button.
Identify the values of a, h, and k from the vertex form of the function. |
\( a = 2 \) \( h = - 5 \) \( k = - 1 \) |
The vertex is located at \( (-5, -1) \). Since the value of \( a = 2 \), the transformed graph will open up, and it will be stretched taller than the parent graph. Use the key points from the parent function and the value of a to help you create the transformed graph. Notice how you can see the location of the vertex by reading the graph. You can also see that this parabola opens up and is stretched taller than the parent quadratic function. This matches the information you read from the function. |
|
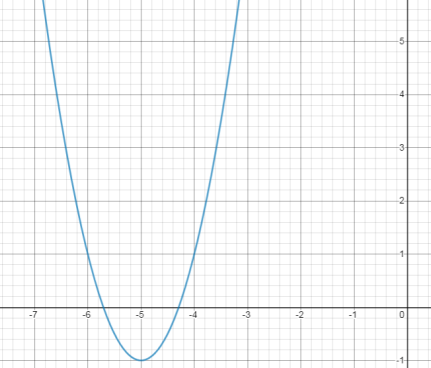
Graph \( g\left( x \right) = - 2x^{2} + 8x + 5 \) using transformations.
The graph is shown. The blue curve is \( g\left( x \right) = - 2x^{2} + 8x + 5 \). The red curve is the parent function. It is shown for reference.
If you need help arriving at this answer, click the solution button.
The given function is not in vertex form. You need to rewrite it. |
Isolate the c term. \( g\left( x \right) = - 2x^{2} + 8x + 5 \) \( g\left( x \right) = - 2{(x}^{2} - 4x) + 5 \) Find the value of \( \left( \frac{b}{2} \right)^{2} \). \( \left( \frac{4}{2} \right)^{2} = 2^{2} = 4 \) Carefully add the value of \( \left( \frac{b}{2} \right)^{2} \) both inside and outside the parentheses. You added \( -2(4) = -8 \) inside the parentheses, so you need to add 8 to the c term to keep the equation balanced. Then simplify. \( g\left( x \right) = - 2\left( x^{2} - 4x + 4 \right) + 5 + 8 \) \( g\left( x \right) = - 2\left( x - 2 \right)^{2} + 13 \) |
Identify the values of a, h, and k from the vertex form of the function. |
\( a = - 2 \) \( h = 2 \) \( k = 13 \) |
The vertex is located at (2, 13). Since the value of \( a = - 2 \), the transformed graph will open down, and it will be stretched taller than the parent graph. Use the key points from the parent function and the value of a to help you create the transformed graph. Notice how you can see the location of the vertex by reading the graph. You can also see that this parabola opens down and it is stretched taller than the parent quadratic function. This matches the information you read from the function. |

|
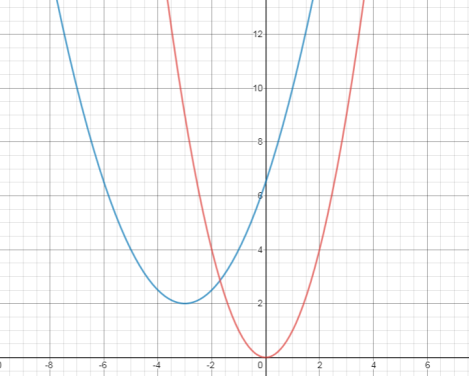
Graph \( h\left( x \right) = \frac{1}{2}\left( x + 3 \right)^{2} + 2 \) using transformations.
The graph is shown. The blue curve is \( h\left( x \right) = \frac{1}{2}\left( x + 3 \right)^{2} + 2 \). The red curve is the parent function. It is shown for reference.
If you need help arriving at this answer, click the solution button.
Identify the values of a, h, and k from the vertex form of the function. |
\( a = \frac{1}{2} \) \( h = 3 \) \( k = 2 \) |
The vertex is located at (-3, 2). Since the value of \( a = \frac{1}{2} \), the transformed graph will open up and it will be compressed shorter than the parent graph. Use the key points from the parent function and the value of a to help you create the transformed graph. Notice how you can see the location of the vertex by reading the graph. You can also see that this parabola opens up, and it is compressed shorter than the parent quadratic function. This matches the information you read from the function. |

|
